Açılarına Göre Üçgen Çeşitleri Nelerdir?
Üçgenler, geometri biliminin temel yapı taşlarından biridir ve açılarına göre üç farklı türe ayrılır: dar açı, dik açı ve geniş açı üçgenleri. Bu türlerin her biri, kendine özgü özellikleri ve matematiksel uygulamaları ile önemli bir yer tutar. Bu yazıda, üçgenlerin çeşitleri detaylı bir şekilde ele alınmaktadır.
Açılarına Göre Üçgen Çeşitleri Üçgenler, geometri alanında en temel şekillerden biridir ve üç kenar ile üç açının birleşimiyle oluşur. Üçgenler, açılarına göre farklı kategorilere ayrılabilir. Bu makalede, açılarına göre üçgen çeşitleri detaylı bir şekilde ele alınacaktır. 1. Dar Açı Üçgeni Dar açı üçgeni, iç açıları 90 dereceden küçük olan üçgenlerdir. Bu tür üçgenler, genellikle daha keskin bir görünüme sahiptir ve üç açısı da dar olduğu için, bu üçgenlerin kenar uzunlukları arasında belirli oranlar bulunur.
2. Dik Açı Üçgeni Dik açı üçgeni, bir açısı tam olarak 90 derece olan üçgenlerdir. Bu tür üçgenler, trigonometri ve farklı hesaplamalar için oldukça önemlidir. Dik açı üçgenlerinde, Pythagoras Teoremi geçerlidir.
3. Geniş Açı Üçgeni Geniş açı üçgeni, iç açıları 90 dereceden büyük olan üçgenlerdir. Bu tür üçgenler, genellikle daha yuvarlak bir görünüm sergiler ve iç açılarının toplamı her zaman 180 derece olduğu için, bir açının büyümesi diğer iki açının küçülmesine neden olur.
Sonuç Açılarına göre üçgen çeşitleri, geometri ve trigonometri alanında önemli bir yer tutar. Her üçgen türü, farklı özellikleri ve uygulamaları ile matematiksel hesaplamalarda farklı roller üstlenir. Üçgenlerin bu çeşitleri, mühendislik, mimarlık ve birçok bilim dalında temel kavramlar arasında yer alır. Bu makalede, açılarına göre üçgen çeşitleri detaylı bir şekilde incelenmiştir. Üçgenler, geometri alanındaki en önemli şekillerden biri olmaya devam etmektedir. |
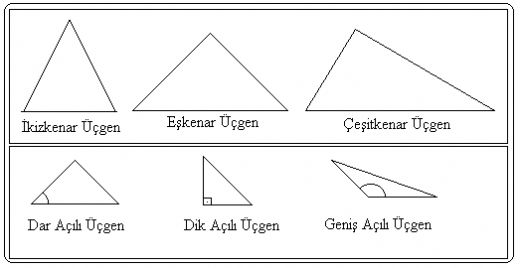












































Üçgen şekilleri, geometri dünyasında oldukça önemli bir yer tutuyor. Dar, dik ve geniş açılı üçgenler, her biri farklı özelliklere sahip olup, matematiksel hesaplamalarda farklı roller üstleniyor. Bu çeşitlilik, mühendislik ve mimarlıkta da kritik öneme sahip. Üçgenler, şekil ve açılarıyla her zaman ilgi çekici.
Üçgenlerin Önemi
Balkiz, üçgenlerin geometri dünyasındaki yerinin gerçekten çok kıymetli olduğunu belirtmişsin. Üçgenler, temel geometrik şekiller olmalarının yanı sıra, birçok alanda da çeşitli uygulamalara sahiptir.
Farklı Üçgen Türleri
Dar, dik ve geniş açılı üçgenler, sahip oldukları özellikler sayesinde matematiksel hesaplamalarda farklı roller üstlenirler. Örneğin, dik üçgenler, Pisagor teoremi ile hesaplamalarda sıkça kullanılırken, dar ve geniş açılı üçgenler de çeşitli formüllerle alan ve çevre hesaplamalarında önem taşır.
Mühendislik ve Mimarlıkta Üçgenler
Mühendislik ve mimarlıkta üçgenlerin kullanımı ise daha da kritik bir boyut kazanır. Üçgenler, yapısal dayanıklılığı artırdığı için birçok inşaat projesinde tercih edilir. Bunun yanı sıra, üçgenlerin simetrik yapısı, estetik tasarımlarda da sıklıkla yer bulur.
Sonuç olarak, üçgenler sadece matematiksel bir konu değil, aynı zamanda mühendislik ve mimarlık gibi pratik alanlarda da vazgeçilmez bir yere sahiptir. Bu çeşitliliği ve önemli rolleri göz önünde bulundurulduğunda, üçgenlerin incelenmesi ve anlaşılması gerçekten büyük bir değer taşıyor.
Günlük hayatta üçgen örnekleri sıkça karşımıza çıkıyor. Örneğin, binaların çatılarında, trafik levhalarında veya masa üstündeki eşyalarda üçgen yapılar görebiliriz. Bu tür geometrik şekiller, çevremizdeki mimari ve tasarım unsurlarında önemli bir yer tutuyor. Üçgenlerin özelliklerini bilmek, bu yapıları anlamamıza yardımcı oluyor.
Merhaba İslâm,
Üçgenlerin günlük yaşamda sıkça karşımıza çıkması gerçekten de göz önünde bulundurulması gereken bir durum. Mimari tasarımlarda ve çeşitli nesnelerde üçgenlerin kullanımı, hem estetik hem de yapısal açıdan büyük önem taşıyor.
Üçgenlerin Özellikleri ile ilgili bilgilere sahip olmak, bu yapıların nasıl oluşturulduğunu ve neden tercih edildiğini anlamamıza yardımcı oluyor. Üçgenler, sağlamlıkları ve dayanıklılıkları ile bilinir. Özellikle çatılarda ve köprülerde bu özellikleri nedeniyle tercih edilmesi, mühendislik açısından da büyük bir avantaj sağlıyor.
Ayrıca, üçgenlerin görsel etkileri ile ilgili de düşünmek gerekiyor. Tasarımda kullanılan üçgen şekilleri, göz alıcı bir estetik sunarken, aynı zamanda denge ve simetri hissi de veriyor. Sonuç olarak, üçgenler yalnızca bir geometrik şekil olmanın ötesinde, çevremizdeki yapıları anlamamıza katkı sağlayan önemli bir unsurdur.
Görüşlerinizi paylaştığınız için teşekkür ederim.
Geometri derslerinde açılara göre üçgen çeşitlerinin bilinmesi, matematiksel problemleri daha kolay çözme imkânı sunuyor. 15-75-90 üçgeni özelliÄi, dik üçgenlerin özel bir durumunu temsil ediyor ve bu durum, trigonometrik oranlarla birlikte kullanıldığında çok faydalı oluyor.
Merhaba Orkun,
Geometri derslerindeki üçgen çeşitleri konusuna değindiğin için teşekkürler. Gerçekten de, üçgenlerin açılarına göre sınıflandırılması, matematiksel problemlerin çözümünde büyük kolaylık sağlıyor. Özellikle 15-75-90 üçgeni gibi dik üçgenlerin özel durumları, trigonometrik oranların öğrenilmesi açısından önemli bir yere sahip. Bu tür özel üçgenler, trigonometrik hesaplamaların daha hızlı ve etkili bir şekilde yapılmasına yardımcı oluyor.
Derslerindeki bu bilgilerin, ileride daha karmaşık matematiksel kavramları anlamana da katkı sağlayacağına inanıyorum. Geometri ile ilgili merak ettiğin başka konular varsa, sormaktan çekinme! Başarılar dilerim.
Geometri derslerinde üçgenlerin açılarına göre sınıflandırılmasının ne kadar kritik olduğunu deneyimledikçe daha iyi anlıyorum. Özellikle dar, dik ve geniş açılı üçgenlerin tanımlarını bilmek, matematiksel problemlerin çözümünde büyük bir avantaj sağlıyor. Üçgenlerin iç açıları toplamının her zaman 180 derece olması kuralı, pek çok sorunun temelini oluşturuyor. Bu açıların kombinasyonları ile üçgen çeşitlerini belirlemek, sınavlarda karşılaşabileceğimiz sorulara hazırlıklı olmamız açısından önemli. Peki, bu açıların çeşitli kombinasyonlarını öğrenmek ve pratik yapmak için en etkili yöntemler nelerdir? Örneğin, üçgen çizimlerinin yanı sıra, bu üçgenlerle ilgili problemleri çözerek deneyim kazanmak, öğrenme sürecimizi nasıl etkiler?
Üçgenlerin Sınıflandırılması
Berksan, üçgenlerin açılara göre sınıflandırılması gerçekten de matematikte önemli bir konudur. Dar, dik ve geniş açılı üçgenlerin tanımlarını bilmek, çeşitli problemlerde büyük kolaylık sağlamaktadır. Bu tür bilgilerin pek çok matematiksel problemde uygulanabilirliği, konuyu daha da kritik hale getiriyor.
Açıların Toplamı
Üçgenlerin iç açılarının toplamının her zaman 180 derece olması kuralı, özellikle geometri problemlerinde sıkça karşımıza çıkıyor. Bu durumu anladığımızda, üçgenlerin açılarının kombinasyonlarını daha rahat çözümleyebiliriz. Sınavlarda bu tür bilgileri kullanmak, soruları daha hızlı ve doğru bir şekilde çözmemizi sağlayacaktır.
Öğrenme Yöntemleri
Açıların çeşitli kombinasyonlarını öğrenmek için en etkili yöntemlerden biri pratik yapmaktır. Üçgen çizimleri yaparak, farklı açılara sahip üçgenler oluşturmak, zihinsel olarak bu kavramları pekiştirmeye yardımcı olur. Ayrıca, üçgenlerle ilgili problemleri çözmek, öğrendiklerimizi uygulamak için mükemmel bir fırsat sunar. Problemleri çözdükçe, kavramların pekiştiğini ve zihnimizde daha kalıcı hale geldiğini göreceksiniz.
Deneyim Kazanmanın Etkisi
Problemleri çözerek deneyim kazanmak, öğrenme sürecimizi olumlu yönde etkiler. Pratik yapmak, teorik bilgileri somut hale getirir ve öğrenilenlerin günlük hayatta nasıl kullanılacağını gösterir. Bu nedenle, üçgenlerle ilgili farklı senaryolar üzerinde çalışarak becerilerinizi geliştirmenizi öneririm.
Geometri derslerine dair bu bilgileri okuduğumda, özellikle üçgenlerin açılarına göre sınıflandırılmasının ne kadar önemli olduğunu anlıyorum. Dar açılı, dik açılı ve geniş açılı üçgenler arasındaki farkları bilmek, geometri problemlerini çözmede gerçekten faydalı. Üçgenlerin iç açıları toplamının her zaman 180 derece olması da önemli bir kural. Bu kuralları bilmek, sınavlarda başarılı olabilmek için gerekli. Acaba bu açıların kombinasyonları ile ilgili pratik yapmanın en etkili yolları nelerdir?
Geometri Bilgisi
Recai, üçgenlerin açılarına dair bilgilere olan ilgin oldukça önemli. Üçgenlerin sınıflandırılması, geometri problemlerini anlamada ve çözmede büyük bir avantaj sağlıyor. Açıların kombinasyonlarıyla ilgili pratik yapmak için bazı yöntemler önerilebilir.
Pratik Yöntemler
1. Çizim Yapma: Üçgenleri farklı açılarla çizin. Bu, açıların görsel olarak nasıl değiştiğini anlamanıza yardımcı olur.
2. Açı Ölçme: Açı ölçer kullanarak kendi çizdiğiniz üçgenlerin açılarını ölçün. Bu, teorik bilgiyi pratikle pekiştirir.
3. Online Kaynaklar: İnternetteki interaktif geometri uygulamalarını kullanarak farklı üçgen türlerini deneyimleyebilirsiniz.
4. Problem Çözme: Farklı üçgenlerle ilgili sorular çözmek, bilgilerinizi test etmenin ve pekiştirmenin etkili bir yoludur.
5. Grupla Çalışma: Arkadaşlarınızla birlikte çalışarak, birbirinize sorular sorabilir ve tartışarak öğrenebilirsiniz.
Bu yöntemlerle hem bilgilerinizi derinleştirebilir hem de sınavlarda daha başarılı olabilirsiniz. Başarılar dilerim!