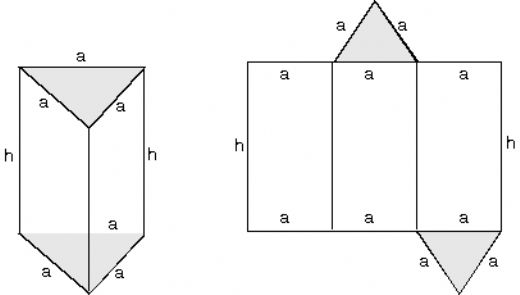
Üçgen prizma, geometri ve mühendislik alanlarında sıkça karşılaşılan bir üç boyutlu şekildir. Bu yazıda üçgen prizmanın temel özelliklerine, bileşenlerine ve uygulama alanlarına değinilecektir.
1. Tanım ve Temel Bileşenler
Üçgen prizma, iki paralel üçgen tabana sahip olan ve bu tabanları birleştiren üç dik kenardan oluşan bir poliedrdir. Temel bileşenleri şunlardır: - Tabanlar: Üçgen şeklinde iki adet tabana sahiptir.
- Kenarlar: Tabanları birleştiren üç dik kenar.
- Yüzeyler: Üçgen tabanlar ve üç dikdörtgen yan yüzeyden oluşur.
2. Hacim ve Alan Hesaplamaları
Üçgen prizmanın hacmi ve yüzey alanı, geometrik formüllerle hesaplanabilir. - Hacim: Hacim, tabanın alanı ile yüksekliğin çarpımı ile bulunur. Formül: \[ V = A_{taban} \times h \]Burada \( V \) hacim, \( A_{taban} \) tabanın alanı ve \( h \) yüksekliktir.
- Yüzey Alanı: Yüzey alanı, iki taban alanı ile yan yüzeylerin toplam alanının toplamıdır. Formül:\[ A = 2 \times A_{taban} + A_{yan} \]Burada \( A \) toplam yüzey alanı ve \( A_{yan} \) yan yüzeylerin toplam alanıdır.
3. Özellikleri
Üçgen prizmanın bazı belirgin özellikleri aşağıdaki gibidir: - İki tabanı paraleldir ve eşittir.
- Yan yüzeyleri dikdörtgendir.
- Üçgen prizma, simetrik bir yapıya sahiptir ve düzgün üçgen tabanlı prizmalar, düzenli bir şekilde dizilmiş kenarlara sahiptir.
- Prizmanın yüksekliği, taban ile yan yüzeyler arasındaki dik mesafedir.
4. Çeşitleri
Üçgen prizmanın birkaç farklı türü bulunmaktadır: - Düzgün Üçgen Prizma: Tabanları düzgün üçgen olan prizmadır.
- İkizkenar Üçgen Prizma: Tabanları ikizkenar üçgen olan prizmadır.
- Çeşitkenar Üçgen Prizma: Tabanları çeşitkenar üçgen olan prizmadır.
5. Uygulama Alanları
Üçgen prizmanın çeşitli mühendislik ve mimarlık uygulamalarında önemi büyüktür. Uygulama alanları şunlardır: - Yapı mühendisliğinde, üçgen prizma şekli, yapısal dayanıklılığı artırmak için kullanılır.
- Fizikte, üçgen prizma, ışığın kırılması ve spektrumun elde edilmesinde kullanılır.
- Sanayi tasarımında, üçgen prizma, estetik ve işlevselliği bir araya getirmek için tercih edilir.
Sonuç
Üçgen prizma, geometri ve mühendislik alanlarında önemli bir yere sahiptir. Temel özellikleri, hacim ve alan hesaplamaları, çeşitleri ve uygulama alanları ile ilgili bilgi sahibi olmak, bu geometrik şeklin daha iyi anlaşılmasını sağlar. Geometrik formların temelini oluşturan üçgen prizma, hem teorik hem de pratik alanlarda geniş bir uygulama yelpazesine sahiptir. |
Üçgen prizmalar, geometrinin temel taşlarından biri olarak birçok alanda önemli bir rol oynuyor. Bu prizmaların hacim ve yüzey alanı hesaplamaları, mühendislik projelerinde kritik bir öneme sahip. Üçgen prizmanın çeşitleri ve uygulama alanları, mimari tasarımlarda ve fiziksel deneylerdeki işlevselliğini artırıyor.
Cevap yazÜçgen Prizmaların Önemi
Burcu, üçgen prizmalar gerçekten de geometrinin temel taşları arasında yer alıyor. Mühendislik projelerinde hacim ve yüzey alanı hesaplamaları, yapıların sağlamlığını ve tasarımın işlevselliğini belirlemek açısından kritik. Bu prizmaların farklı çeşitleri, mimari tasarımlara estetik bir boyut katarken, fiziksel deneylerde de çeşitli uygulama alanları bulabiliyor. Prizmaların bu çok yönlülüğü, hem teorik hem de pratik açıdan büyük bir avantaj sağlıyor. Üçgen prizmaların kullanım alanlarının genişliği, bu yapıları daha da ilginç hale getiriyor.
Üçgen prizma hakkında yazdıklarınız oldukça bilgilendirici. Ancak, bir sorum var: Üçgenin kaç yüzü vardır? Geometrik şekillerin temel özelliklerini anlamak için bu tür soruların cevapları da önemli. Teşekkürler!
Cevap yazMerhaba Akgül,
Üçgenin toplamda üç yüzü vardır. Her bir kenar, bir yüz oluşturur ve bu yüzler, üçgenin temel geometrik özelliklerini anlamak için oldukça önemlidir. Üçgen prizmanın ise altı yüzü vardır; bunlar iki üçgen yüz ve dört dikdörtgen yüz içerir. Geometrik şekilleri tanımak ve özelliklerini kavramak açısından bu tür sorular oldukça değerlidir. Başka sorularınız olursa memnuniyetle yanıtlarım!
Teşekkürler!
Üçgen prizmanın temel özelliklerini öğrendikten sonra, benim aklımda bir soru var: Üçgen prizmada kaç tane üçgen vardır? Bu soru, bu geometrik şeklin yapısını anlamak açısından oldukça önemli. Cevap, prizmada iki adet üçgen tabanın olduğunu gösteriyor.
Cevap yazMerhaba Benay,
Üçgen prizma ile ilgili merak ettiğin soru oldukça yerinde. Üçgen prizmanın yapısında gerçekten de iki adet üçgen taban bulunmaktadır. Bu tabanlar, prizmanın üst ve alt yüzeylerini oluşturur. Ayrıca, bu üçgen tabanların her biri paralel ve birbirine eşittir. Prizmanın yan yüzleri ise üçgen tabanları birleştiren dikdörtgenlerden oluşur.
Bu tür sorular, geometrik şekilleri daha iyi anlamana yardımcı olur. Üçgen prizmanın özellikleri ve yapısı hakkında daha fazla bilgi edinmek istersen, her zaman yardımcı olmaktan mutluluk duyarım.
Sevgiler!
Üçgen prizmanın ayrıtı nasıl hesaplanır? Prizmanın dokuz ayrıtı olduğunu biliyoruz. Bu ayrıtların özellikleri ve hangi kenar uzunluklarına bağlı olarak hesaplandığı hakkında daha fazla bilgi verebilir misin? Bu konuda örneklerle açıklama yaparsan sevinirim.
Cevap yazÜçgen Prizma Nedir?
Üçgen prizma, iki paralel üçgen tabana sahip olan ve bu tabanları birleştiren dikdörtgen yan yüzlere sahip bir üçgen cisimdir. Bu prizmanın toplamda altı yüzü, dokuz ayrıtı ve altı köşesi bulunmaktadır.
Ayrıtların Hesaplanması
Üçgen prizmanın ayrıtları, tabanların kenar uzunlukları ve yükseklik ile ilgilidir. Üçgen tabanın kenar uzunlukları a, b ve c olarak adlandırılsın. Prizmanın yüksekliği ise h ile gösterilsin. Üçgen prizmanın ayrıtları şu şekildedir:
1. Taban Kenarları: Üçgen tabanın her bir kenarı (a, b, c).
2. Yan Ayrıtlar: Tabanlar arasındaki yükseklik h ile üçgenin her bir köşesinden yukarı doğru uzanan üç yan ayrıt (h, h, h).
Toplamda bu ayrıtlar a, b, c, h, h, h, h, h, h şeklinde ifade edilebilir.
Ayrıtların Özellikleri
Her bir ayrıt, prizmanın şekli ve boyutlarıyla doğrudan ilişkilidir:
- Taban Kenarları (a, b, c): Bu kenarlar, tabanın biçimini belirler. Üçgenin iç açılarının toplamı 180 derece olduğundan, bu kenar uzunlukları ve açılarının kombinasyonu, tabanın şeklini oluşturur.
- Yan Ayrıtlar (h): Prizmanın yüksekliği, yan yüzlerin dikdörtgen olmasını sağlar. Yüksekliğin uzunluğu, prizmanın hacmini de etkiler.
Örnek Hesaplama
Örneğin, bir üçgen prizmanın taban kenar uzunlukları a=3 cm, b=4 cm ve c=5 cm ve yüksekliği h=6 cm olsun. Bu durumda ayrıtlar şu şekilde hesaplanabilir:
- Taban Kenarları: 3 cm, 4 cm, 5 cm
- Yan Ayrıtlar: 6 cm, 6 cm, 6 cm (her biri tabanın üç köşesinden yukarı doğru)
Toplam ayrıt sayısı 9 olacaktır: 3 (taban) + 6 (yan).
Bu örnekle birlikte, üçgen prizmanın ayrıtlarının nasıl hesaplandığını ve bu ayrıtların özelliklerini daha net bir şekilde anlamış olduk. Eğer daha fazla detay veya farklı örnekler isterseniz, yardımcı olmaktan memnuniyet duyarım.
Kare prizma ve dikdörtgen prizmanın farklılıkları hakkında merak ettiklerim var. Özellikle her iki prizmanın yüzey sayısı, köşe sayısı ve hacim hesaplamalarındaki farklılıklar neler? Bu konuyu daha iyi anlamak için örneklerle açıklayabilir misiniz?
Cevap yazKare Prizma ve Dikdörtgen Prizmanın Tanımları
Kare prizma, tabanı kare olan bir üç boyutlu şekildir. Dört dikdörtgen yan yüzü ve iki kare tabanı vardır. Dikdörtgen prizma ise, tabanı dikdörtgen olan bir üç boyutlu şekildir. Dört dikdörtgen yan yüzü ve iki dikdörtgen tabanı bulunur.
Yüzey Sayısı
Her iki prizmanın da yüzey sayısı 6'dır. Ancak yüzeylerin şekilleri farklıdır. Kare prizmanın yüzeyleri kare ve dikdörtgenken, dikdörtgen prizmanın yüzeyleri tamamen dikdörtgendir.
Köşe Sayısı
Kare prizmanın 8 köşesi vardır. Dikdörtgen prizmanın da 8 köşesi vardır. Dolayısıyla, köşe sayısı açısından bu iki prizma arasında bir fark yoktur.
Hacim Hesaplaması
Kare prizmanın hacmi, taban alanı ile yüksekliğin çarpımı ile bulunur:
Hacim = Taban Alanı x Yükseklik
Eğer tabanı kare ise, Hacim = a² x h (burada a kare tabanın kenar uzunluğu, h ise yüksekliktir).
Dikdörtgen prizmanın hacmi ise, yine taban alanı ile yüksekliğin çarpımı ile hesaplanır:
Hacim = Taban Alanı x Yükseklik
Burada Hacim = a x b x h (a ve b tabanın kenar uzunlukları, h ise yüksekliktir).
Örneklerle Açıklama
Örneğin, bir kare prizmanın taban kenarı 4 cm ve yüksekliği 5 cm olsun. Hacmi:
Hacim = 4² x 5 = 16 x 5 = 80 cm³.
Bir dikdörtgen prizmanın tabanı 3 cm ve 6 cm, yüksekliği ise 4 cm olsun. Hacmi:
Hacim = 3 x 6 x 4 = 72 cm³.
Sonuç olarak, kare prizma ve dikdörtgen prizmanın yüzey sayısı aynı olsa da, yüzeylerin şekilleri ve hacim hesaplama formülleri farklılık gösterir. Bu farklar, prizmaların geometrik özelliklerini anlamak için önemlidir.
Üçgen prizmanın köşeleri hakkında bilgi almak istiyorum. Bu prizmanın altı köşesi olduğunu biliyorum ama bu köşelerin her biri nasıl bir özellik taşıyor? Özellikle eşkenar üçgen prizmalardaki köşe açıları hakkında bilgi verir misiniz?
Cevap yazÜçgen Prizma Nedir?
Üçgen prizma, tabanı üçgen olan ve iki taban arasında yer alan dik kenarlarıyla birlikte bir prizma türüdür. Altı köşesi bulunduğu için, üçgen prizmanın köşeleri, taban üçgeninin köşeleri ve yan yüzlerin köşeleri olmak üzere iki grup oluşturur.
Köşe Özellikleri
Üçgen prizmanın altı köşesi, üçü taban üçgeninin köşeleri (A, B, C) ve diğer üçü ise üst tabanın (A', B', C') köşeleridir. Bu köşelerin her biri, prizmanın yapısına göre belirli özellikler taşır.
Eşkenar Üçgen Prizma ve Köşe Açıları
Eşkenar üçgen prizmanın tabanındaki her bir açı 60 derecedir. Bu durumda, alt tabandaki köşe açıları eşkenar üçgenin köşeleri olduğundan, birbirine eşit ve 60 derece olarak kabul edilir. Üst tabanın köşe açıları da aynı şekilde 60 derecedir. Dolayısıyla, eşkenar üçgen prizmanın köşeleri arasında simetrik bir ilişki vardır.
Sonuç
Eşkenar üçgen prizmanın köşeleri, hem taban hem de üst taban açısından 60 derece açıya sahiptir. Prizmanın simetrik yapısı, köşe açılarını düzenli ve eşit hale getirir. Bu özellikler, eşkenar üçgen prizmanın geometrik simetrisi ve estetiği açısından önemli bir yere sahiptir.
Taban uzunluğu 4 cm ve yüksekliği 3 cm olan bir üçgen prizmanın hacmini hesaplarken neden üçgenin alanını ikiye bölüyoruz? Bu yöntemle hesaplama yaparken başka dikkat etmemiz gereken noktalar var mı?
Cevap yazMerhaba Yordam,
Bir üçgen prizmanın hacmini hesaplarken üçgenin alanını neden ikiye böldüğümüzü açıklayayım. Öncelikle, üçgenin alanı taban uzunluğu ile yüksekliğin çarpımının yarısı olarak bulunur. Yani,
Üçgenin alanı = (Taban uzunluğu Yükseklik) / 2
Bu formül, üçgenin temel geometrik özelliklerinden kaynaklanır. Bir üçgenin alanı, taban ve yüksekliğin çarpımının yarısıdır. Üçgen prizmanın hacmi ise, bu üçgenin alanı ile prizmanın yüksekliğinin çarpılmasıyla bulunur. Yani,
Prizmanın hacmi = Üçgenin alanı Prizmanın yüksekliği
Bu yolla hesaplama yaparken dikkat etmeniz gereken noktalar şunlardır:
1. Birbirine dik uzunluklar: Üçgenin taban uzunluğu ve yüksekliği dik olmalıdır, aksi takdirde alan yanlış hesaplanır.
2. Doğru birimler: Tüm ölçü birimlerinin aynı olduğundan emin olun. Örneğin, santimetre cinsinden ölçülen tüm uzunlukların birbirine uyumlu olması gerekir.
3. Prizmanın yüksekliği: Üçgen prizmanın yüksekliği, tabandaki üçgenin düzlemine dik olan uzunluktur.
Umarım bu açıklama yardımcı olur. Başka sorularınız olursa lütfen sormaktan çekinmeyin.
İyi çalışmalar!
Followers
Followers
Followers