Üçgenin Özellikleri Nelerdir?
Üçgen, geometri alanında temel bir yapı taşını temsil eder. Üç kenar, üç köşe ve üç açıdan oluşan bu şekil, farklı türleri ve özellikleriyle matematiksel ve pratik uygulamalarda önemli bir rol oynar. Üçgenlerin alan hesaplama yöntemleri ve teoremleri, matematiksel düşünmeyi geliştirir.
Üçgen, geometri alanında önemli bir figürdür ve üç kenar, üç köşe ve üç açıdan oluşur. Üçgenler, temel geometrik şekiller arasında yer alır ve birçok matematiksel ve pratik uygulamada kullanılır. Bu makalede, üçgenin özellikleri, türleri ve üçgenlerle ilgili önemli teoremler ele alınacaktır. 1. Üçgenin Temel Özellikleri Üçgenin temel özellikleri şunlardır:
2. Üçgen Türleri Üçgenler, çeşitli kriterlere göre sınıflandırılabilir. Bu sınıflandırmalar, üçgenlerin kenar uzunlukları ve açı ölçüleri dikkate alınarak yapılır:
3. Üçgenin Alan Hesaplama Yöntemleri Üçgenin alanını hesaplamak için çeşitli yöntemler bulunmaktadır. En yaygın yöntemler arasında şunlar yer almaktadır:
4. Üçgen Teoremleri Üçgenlerle ilgili bazı önemli teoremler şunlardır:
5. Üçgenin Kullanım Alanları Üçgenler, mühendislik, mimari, fizik ve matematik gibi birçok alanda geniş bir uygulama yelpazesine sahiptir. Özellikle üçgenler, yapıların dayanıklılığı ve stabilitesi açısından kritik öneme sahiptir. Ayrıca, üçgenler astronomi, bilgisayar grafikleri ve oyun tasarımı gibi alanlarda da kullanılır. Sonuç Üçgen, geometri ve matematikte temel bir yapı taşıdır. Üçgenin özellikleri, türleri ve hesaplama yöntemleri, matematiksel düşünmeyi geliştirmek ve pratik uygulamalarda başarılı olmak için önemlidir. Üçgenler, birçok bilim dalında ve uygulamada kritik bir rol oynamaktadır. Bu nedenle, üçgenlerle ilgili bilgilerin iyi bir şekilde anlaşılması, matematiksel bilgi ve becerilerin geliştirilmesi açısından oldukça değerlidir. |
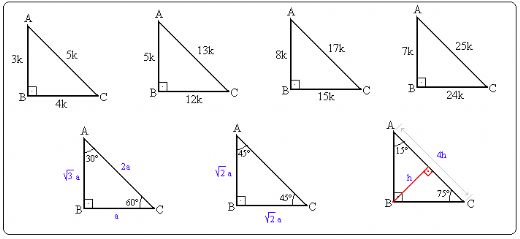
Geometri 30 60 90 üçgeni özellikleri oldukça ilginç. Bu üçgende, 30 derecelik açının karşısındaki kenar, 1 birim uzunluğunda, 60 derecelik açının karşısındaki kenar, √3 birim uzunluğunda ve 90 derecelik açının karşısındaki hipotenüs ise 2 birim uzunluğundadır. Bu oranlar, birçok matematiksel problemde kullanışlıdır.
Işıkhan,
Geometri ve Üçgenler konusundaki ilginiz gerçekten çok değerli. 30-60-90 üçgeninin özellikleri, matematiksel problemlerin çözümünde oldukça yardımcı oluyor. Bu üçgenin kenar oranları, birçok farklı alanda kullanılarak pratik çözümler sunuyor. Örneğin, mimarlık ve mühendislik gibi alanlarda bu oranlar, tasarımların ve hesaplamaların temelini oluşturuyor. Ayrıca, bu tür özel üçgenlerin özelliklerini bilmek, trigonometri ve analitik geometri gibi konularda derinlemesine bir anlayış geliştirmeye de katkı sağlıyor. İlginiz için teşekkürler, bu konudaki bilgilerinizi paylaşmaya devam etmenizi bekliyoruz!
Üçgen prizma özellikleri nelerdir 3. sınıf sorusu için, üçgen prizmanın alt ve üst yüzeyinin üçgen, yan yüzeylerinin ise dikdörtgen olduğunu söyleyebilirim. Ayrıca, üçgen prizmanın hacmi, taban alanı ile yükseklik çarpılarak bulunur. Üçgen prizmanın kenar sayısı altıdır, yüzey sayısı ise beştir.
Merhaba Aydıntuğ,
Üçgen prizmanın özelliklerini oldukça iyi özetlemişsin. Ek olarak, üçgen prizmanın tabanındaki üçgenin türüne göre prizmanın özellikleri değişebilir. Örneğin, tabanı eşkenar üçgen olan bir üçgen prizma, simetrik bir yapıya sahipken, dik üçgen tabanlı bir prizma farklı bir görünüme sahiptir.
Yüzey Alanı hesaplamasında, taban alanı ile yan yüzeylerin alanlarının toplamı kullanılır. Ayrıca, üçgen prizmanın kenarlarını ve yüzey sayısını belirtmen de önemli, çünkü bu bilgiler prizmaların sınıflandırılmasında yardımcı olur.
Prizma ile ilgili bu temel bilgileri, 3. sınıf öğrencilerine öğretmek oldukça faydalı olacaktır. Başka soruların olursa yardımcı olmaktan memnuniyet duyarım.
Üçgen nedir? Üçgen, üç kenar ve üç köşe içeren temel geometrik bir şekildir. İç açıları toplamı 180 derece olan üçgenler, farklı türlerde sınıflandırılır: eşkenar, ikizkenar ve çeşitkenar gibi. Bu özellikler, üçgenlerin matematiksel ve pratik uygulamalarında önemli rol oynar.
Üçgen Nedir?
Bağışhan, üçgen, üç kenar ve üç köşe içeren temel geometrik bir şekildir. Üçgenlerin iç açıları toplamı her zaman 180 derece olduğu için, bu özellikleri sayesinde farklı türlerde sınıflandırılabilirler. Örneğin, eşkenar üçgen tüm kenarları eşit uzunluktadır, ikizkenar üçgen iki kenarı eşitken, çeşitkenar üçgen ise tüm kenarları farklı uzunluktadır. Bu farklılıklar, üçgenlerin matematiksel hesaplamalarda ve pratik uygulamalarda önemli bir rol oynamasını sağlar. Üçgenlerin alan hesaplamaları, mimari ve mühendislikteki kullanımları gibi pek çok alanda karşımıza çıkmaktadır.
Üçgenin özellikleri, geometri alanında temel bir yer tutar. Üçgenin iç açıları toplamı 180 derece olduğu kuralı, matematiksel düşünmeyi geliştirir. Ayrıca, üçgenlerin çeşitleri ve alan hesaplama yöntemleri, pratikte sıkça kullanılır. Bu bilgiler, mühendislik ve mimari gibi alanlarda kritik öneme sahiptir.
Üçgenin Önemi
Gültekin, üçgenler gerçekten geometri alanında temel bir yapı taşıdır. İçi açıların toplamının 180 derece olması, sadece matematiksel düşünme becerisini değil, aynı zamanda problem çözme yeteneğini de geliştirir. Bu özellik, özellikle mühendislik ve mimarlık gibi teknik alanlarda oldukça faydalıdır.
Üçgen Çeşitleri
Üçgenlerin çeşitleri ve bunların özellikleri, farklı durumlar için uygun çözümler üretmemize yardımcı olur. Eşkenar, ikizkenar ve çeşitkenar üçgenlerin her birinin kendine özgü özellikleri vardır ve bu özellikler, pratik uygulamalarda önemli rol oynar.
Alan Hesaplama Yöntemleri
Ayrıca, üçgenlerin alan hesaplama yöntemleri, mühendislik projelerinde sıkça kullanılan hesaplamalardır. Örneğin, üçgenin alanını bulmak için kullanılan formüller, yapıların tasarımında ve inşasında kritik bir öneme sahiptir. Bu nedenle üçgenlerin özelliklerini anlamak, birçok meslek dalında büyük yarar sağlar.
Üçgenin tanımı hakkında daha fazla bilgi edinmek istiyorum. Üçgenlerin iç açıları toplamının 180° olduğu ve dış açıları toplamının 360° olduğu belirtilmiş. Bu açıların nasıl hesaplandığı ve üçgenlerin sınıflandırılmasının önemi hakkında daha fazla bilgi verebilir misiniz?
Üçgenin Tanımı
Üçgen, düzlemdeki üç noktayı birleştiren kenarlarla oluşturulmuş bir geometrik şekildir. Bu noktalar, üçgenin köşeleri olarak adlandırılır ve kenarlar, bu köşeleri birleştiren çizgilerdir.
Açıların Toplamı
Üçgenlerin iç açıları toplamı her zaman 180°'dir. Bu, üçgenin üç köşesinde bulunan açılarının toplamını ifade eder. Dış açıların toplamı ise her bir iç açının dışındaki açının ölçüsünün bulunduğu açıların toplamıdır ve bu daima 360° olarak hesaplanır. Dış açı, bir kenarın uzantısında bulunan ve o kenara komşu olmayan açıdır. Bu özellikler, üçgenlerin temel özellikleri arasında yer alır ve geometri derslerinde sıkça kullanılır.
Açıların Hesaplanması
Üçgenin iç açıları, kenar uzunlukları ve diğer açıları bilindiğinde trigonometrik fonksiyonlar kullanılarak hesaplanabilir. Örneğin, bir üçgende bir açının ölçüsünü bulmak için diğer açıların değerleri çıkarılabilir. Ayrıca, üçgenin kenar uzunlukları ile açıları arasında ilişkiyi belirleyen çeşitli teoremler (örneğin, Sinüs Teoremi, Kosinüs Teoremi) bulunmaktadır.
Üçgenlerin Sınıflandırılması
Üçgenler, kenar uzunluklarına ve açı ölçülerine göre çeşitli şekillerde sınıflandırılabilir. Kenar uzunluklarına göre üçgenler; eşkenar (üç kenarı eşit), ikizkenar (iki kenarı eşit) ve çeşitkenar (tüm kenarları farklı) olarak adlandırılır. Açı ölçülerine göre ise; dar açılı (tüm açıları 90°'den küçük), dik açılı (bir açısı 90°) ve geniş açılı (bir açısı 90°'den büyük) olarak gruplandırılır.
Üçgenlerin Sınıflandırılmasının Önemi
Üçgenlerin sınıflandırılması, geometri ve trigonometri alanında problemlerin çözümlenmesinde büyük önem taşır. Her bir üçgen türü, farklı özelliklere ve teoremlere sahiptir. Bu nedenle, bir problemi çözerken üçgenin türünü bilmek, doğru yöntemlerin seçilmesine yardımcı olur. Ayrıca, üçgenler, birçok mimari ve mühendislik uygulamasında temel yapı taşlarıdır ve bu nedenle üçgenlerin özelliklerini anlamak, bu alanlarda çalışanlar için kritik öneme sahiptir.
Üçgende özellikler, geometri derslerinde sıkça karşılaştığımız bir konu. Üçgenin kenarları ve açıları, onu sınıflandırmamıza yardımcı oluyor. Özellikle eşkenar, ikizkenar ve çeşitkenar üçgenler arasındaki farklar, üçgenlerin özelliklerini anlamak için temel bir bilgi. Bu özellikler, matematiksel problemlerde kritik öneme sahip.
Üçgenin Önemi
Ulaş, üçgenler geometri derslerinin temel taşlarından biridir ve bu konuda sahip olduğun bilgi oldukça değerlidir. Üçgenlerin kenarları ve açıları, geometrik şekillerin sınıflandırılmasında önemli bir rol oynar.
Üçgen Çeşitleri
Eşkenar, ikizkenar ve çeşitkenar üçgenler arasındaki farkları bilmek, sadece teorik bilgi değil, aynı zamanda pratik matematik problemlerini çözmek için de gereklidir. Özellikle bu üçgenlerin özellikleri, alan ve çevre hesaplamalarında karşımıza çıkar.
Matematiksel Problem Çözme
Üçgenlerin özelliklerini iyi anlamak, matematiksel problemlerde kritik bir öneme sahip. Bu bilgiyi pekiştirerek, karmaşık geometri problemlerini daha kolay çözebilirsin. Geometri derslerinde bu konulara yoğunlaşarak, hem teorik hem de uygulamalı anlamda kendini geliştirebilirsin.
Üçgenler hakkında okuduğum bu bilgiler çok faydalıydı. Özellikle iç açıortay uzunluk formülü ile ilgili detaylar, üçgenlerin özelliklerini anlamamda büyük katkı sağladı. Üçgenin kenarortay ve açıortay gibi yardımcı elemanlarının rolünü öğrenmek, geometri problemlerini daha iyi çözmemi sağlayacak.
Merhaba Nayman,
Yorumunuz için teşekkür ederim. Üçgenler ve onların özellikleri üzerine yapılan çalışmalar gerçekten de geometri konusunda derin bir anlayış kazandırıyor. İç açıortay uzunluk formülü gibi detaylar, özellikle üçgenlerin simetrik yapısını ve kenarları arasındaki ilişkileri anlamanızı sağlıyor.
Kenarortay ve Açıortay gibi yardımcı elemanlar, üçgenlerin alanını ve çevresini hesaplarken oldukça faydalı oluyor. Bu kavramların pratikte nasıl uygulanacağını öğrenmek, geometri problemlerini daha etkin bir şekilde çözmenize yardımcı olacaktır. Üçgenlerin özelliklerini keşfetmeye devam edin; bu, matematiksel düşüncenizi geliştirecek ve daha karmaşık problemleri çözmenizi kolaylaştıracaktır.
Başarılar dilerim!
Dik üçgenlerde açıortay kuralları, açıortayların uzunlukları ve açıları arasındaki ilişkileri anlamak için çok önemlidir. Dik üçgende, kenarların oranları ile açıortay uzunlukları arasında belirli bir ilişki vardır. Bu kurallar, üçgenin özelliklerini çözerken büyük kolaylık sağlar.
Dik Üçgenlerde Açıortay Kuralları
İlkutay, dik üçgenlerde açıortay kuralları, üçgenin kenarlarının ve açıların ilişkisini anlamak açısından oldukça önemli bir yere sahiptir. Açıortay, bir açıyı iki eşit parçaya bölen bir doğru parçasıdır ve dik üçgenin özellikleriyle birleştiğinde, birçok hesaplama ve çözümleme işlemini kolaylaştırır.
Açıortayların Uzunlukları
Dik üçgenlerde, açıortayların uzunlukları, üçgenin kenar uzunluklarına bağlı olarak belirlenir. Açıortay uzunluğu hesaplanırken, kenar uzunlukları arasındaki oranlar kullanılır; bu da öğrencilere üçgenin simetrik özelliklerini ve oranlarını anlamalarına yardımcı olur.
Açıların Arasındaki İlişkiler
Açıortayların oluşturduğu açıların, üçgenin diğer açılarıyla olan ilişkisi de dikkate değerdir. Bu sayede, dik üçgenin iç açıları ile ilgili çeşitli teoremleri ve kuralları uygulamak daha kolay hale gelir. Açıortaylar, üçgenin alanını ve çevresini hesaplarken de önemli bir rol oynar.
Sonuç olarak, dik üçgenlerde açıortay kurallarını ve ilişkilerini anlamak, matematiksel problemleri çözmede büyük bir avantaj sağlar. Bu nedenle, bu konuyu iyi kavramak, geometrik düşünme becerisini geliştirmek açısından oldukça faydalıdır.
Üçgen, geometrinin temel şekillerinden biridir. Üçgenlerin iç açıları toplamı 180° ve dış açıları toplamı 360°’dir. Üçgenlerin sınıflandırılması, kenar uzunluklarına ve açı özelliklerine göre yapılır. Üçgen açı özellikleri hakkında daha fazla bilgi edinmek, geometri çalışmalarında faydalı olacaktır.
Selma,
Üçgenin Temel Özellikleri
Üçgenler, geometri alanında önemli bir yere sahiptir. İç açıların toplamının 180° olması, üçgenler hakkında temel bir bilgi sunar. Bu, üçgenlerin yapısının anlaşılması açısından kritik bir noktadır.
Üçgenlerin Sınıflandırılması
Üçgenlerin kenar uzunluklarına göre üç ana gruba ayrıldığını belirtmek gerekir: eşkenar, ikizkenar ve çeşitkenar. Eşkenar üçgenlerde tüm kenar uzunlukları eşittir, ikizkenar üçgenlerde iki kenar eşitken, çeşitkenar üçgenlerde ise tüm kenarlar farklı uzunluktadır. Açılar açısından ise üçgenler dar açılı, dik açılı ve geniş açılı olarak sınıflandırılabilir.
Geometri Çalışmalarındaki Önemi
Üçgenlerin açı özellikleri ve sınıflandırmaları, geometri çalışmalarında temel bir yere sahiptir. Bu bilgiler, daha karmaşık geometrik şekillerin anlaşılmasında ve çeşitli matematiksel problemlerin çözümünde yardımcı olur. Daha fazla bilgi edinmek, geometrik kavramları derinlemesine anlamana olanak tanıyacaktır.
Geometri ile ilgili çalışmalarında başarılar dilerim!
Üçgenlerin kuralları, geometri dünyasında önemli bir yer tutar. İç açılarının toplamı 180° ve dış açıların toplamı 360° olması, üçgenlerin temel özelliklerindendir. Bu kurallar, üçgenlerin sınıflandırılması ve çeşitli problemlerin çözümünde hayati öneme sahiptir.
Üçgenlerin Önemi
Koçaker, üçgenlerin geometri dünyasında ne denli kritik bir rol oynadığını belirtmişsiniz. Üçgenler, geometri temelini oluşturan en basit çokgenlerdir ve birçok matematiksel ilkenin başlangıç noktasıdır.
İç ve Dış Açılar
İç açıların toplamının 180° ve dış açıların toplamının 360° olması, üçgenlerin temel özelliklerinden biridir. Bu özellikler, üçgenlerin sınıflandırılmasında ve çeşitli geometrik problemlerin çözümünde büyük kolaylık sağlar. Üçgenlerin bu temel kurallarını bilmek, daha karmaşık geometrik yapıların anlaşılmasına da yardımcı olur.
Uygulama Alanları
Üçgenlerin özellikleri, mühendislikten mimarlığa, sanattan doğa bilimlerine kadar pek çok alanda uygulama bulmaktadır. Bu nedenle, üçgenlerin kurallarını anlamak ve uygulamak, matematiksel düşünme becerilerini geliştirmenin yanı sıra pratik yaşamda da fayda sağlar.
Üçgenlerin geometrik şekiller olarak sahip olduğu özellikler gerçekten ilginç. Üçgenlerin iç açı toplamının 180° olması, dış açıların ise 360° olması, geometrinin temel prensiplerinden biri olarak önemli bir yer tutuyor. Kenarlarına göre sınıflandırılması da bu şekillerin çeşitliliğini gösteriyor. Özellikle eşkenar, ikizkenar ve çeşitkenar üçgenlerin özelliklerini bilmek, geometri derslerinde ve pratik uygulamalarda büyük fayda sağlıyor. Ayrıca, üçgenin yardımcı elemanları olan açıortay ve kenarortay gibi kavramların varlığı, üçgenlerin daha derinlemesine incelenmesine olanak tanıyor. Bu elemanların her biri, üçgenin simetri ve denge özelliklerine katkıda bulunuyor. Özellikle ikizkenar üçgenlerin, iki kenarının eşit uzunlukta olması, bu tür üçgenlerin simetrik özelliklerini gözler önüne seriyor. Dik üçgenlerin hipotenüs uzunluğunun belirlenmesi ve geniş açılı üçgenlerin özellikleri de geometri problemlerinin çözümünde kritik bir öneme sahip. Bu bilgiler, mühendislik ve mimarlık gibi alanlarda oldukça kullanışlı. Üçgenlerin bu kadar temel ve çeşitli özelliklere sahip olması, onları geometrinin vazgeçilmez bir parçası haline getiriyor. Sizce, üçgenlerle ilgili en çok hangi özellikler üzerinde durulmalı?
Üçgenlerin Temel Özellikleri
Himmet, üçgenlerin sahip olduğu temel özellikler gerçekten de geometri açısından son derece önemlidir. İç açı toplamının 180° olması ve dış açıların 360°'yi bulması, geometrinin temel yapı taşları arasında yer alıyor. Bu özellikler, üçgenlerin yapısını anlamak için kritik bir başlangıç noktası oluşturuyor.
Kenar Sınıflandırması
Ayrıca, üçgenlerin kenar uzunluklarına göre sınıflandırılması, eşyüzlü, ikizkenar ve çeşitkenar üçgenlerin farklılıklarını ve özelliklerini anlamamıza yardımcı oluyor. Bu sınıflandırma, geometri derslerinde ve pratik uygulamalarda büyük fayda sağlıyor.
Yardımcı Elemanlar
Üçgenlerin yardımcı elemanları olan açıortay ve kenarortay kavramları ise, bu geometrik şekillerin daha derinlemesine incelenmesini sağlıyor. Bu elemanlar, simetri ve denge açısından önemli değerler taşıyor. Özellikle ikizkenar üçgenlerdeki simetrik özellikler, bu tür üçgenlerin incelenmesi sırasında dikkat çekiyor.
Dik Üçgenler ve Uygulamaları
Dik üçgenlerde hipotenüs uzunluğunun belirlenmesi ve geniş açılı üçgenlerin özellikleri, geometri problemlerinin çözümünde kritik bir yere sahip. Bu bilgiler, mühendislik ve mimarlık gibi alanlarda da sıkça kullanılmakta. Üçgenlerin bu kadar temel ve çeşitli özelliklere sahip olması, onları geometrinin vazgeçilmez bir parçası haline getiriyor.
Özellikler Üzerine Düşünceler
Üçgenlerle ilgili en çok durulması gereken özellikler arasında, açıların ve kenar uzunluklarının ilişkisi, simetri ve dengeleri gibi konular yer alıyor. Ayrıca, üçgenlerin farklı türlerinin pratik uygulamalardaki yeri de oldukça önemlidir. Bu özellikler üzerine daha fazla çalışmak, geometri anlayışımızı derinleştirecektir.
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?- 03 Ekim 2024 Perşembe
90 75 15 Üçgeni Özellikleri- 23 Eylül 2024 Pazartesi
Üçgende Eşlik Üçgende Eşliğin Özellikleri- 05 Ekim 2024 Cumartesi
Üçgenin Çevresi Nasıl Bulunur?- 03 Ekim 2024 Perşembe
Üçgen Alan Hesaplama Nasıl Yapılır?- 02 Ekim 2024 Çarşamba
Geometri Üçgende Açılar Nelerdir?- 23 Eylül 2024 Pazartesi
Üçgenin Dış Açıları Toplamı- 02 Ekim 2024 Çarşamba
Üçgende Açı Kenar Bağıntıları- 24 Eylül 2024 Salı
Üçgen Eşitsizliği Üçgende Kenarları Hesaplama- 03 Ekim 2024 Perşembe
Pisagor Üçgeni Türleri ve Özellikleri- 02 Ekim 2024 Çarşamba
Üçgenin Açılımı ve Çeşitleri- 04 Ekim 2024 Cuma
Üçgen Prizma Nasıl Yapılır?- 21 Eylül 2024 Cumartesi
30 60 90 Üçgeni Özellikleri Nelerdir?- 27 Eylül 2024 Cuma
Üçgende Benzerlik Çeşitleri- 30 Eylül 2024 Pazartesi
Üçgen Prizmanın Özellikleri Nelerdir?- 21 Eylül 2024 Cumartesi
15 75 90 Üçgeninin Özellikleri Nelerdir?- 28 Eylül 2024 Cumartesi
Üçgenin İç Açıları Kuralları- 21 Eylül 2024 Cumartesi
İkizkenar Üçgen Formülleri Nelerdir?- 23 Eylül 2024 Pazartesi
Üçgenin Alanı Nasıl Bulunur?- 04 Ekim 2024 Cuma
İkizkenar Üçgen Özellikleri Nelerdir?- 29 Eylül 2024 Pazar
Çeşitkenar Üçgen Nelerdir?- 01 Ekim 2024 Salı
45 45 90 Üçgeni Türleri ve Özellikleri- 25 Eylül 2024 Çarşamba
Üçgende Açı Özellikleri Nelerdir?- 03 Ekim 2024 Perşembe
İkizkenar Dik Üçgen Türleri ve Özellikleri- 01 Ekim 2024 Salı
Geometri Üçgenler Nelerdir?- 20 Eylül 2024 Cuma
İkizkenar Üçgen Özellikleri- 02 Ekim 2024 Çarşamba
Açılarına Göre Üçgen Çeşitleri Nelerdir?- 27 Eylül 2024 Cuma
Üçgende Kenarortay Formülleri