
Üçgenin İç Açıları Kuralları
Üçgenin iç açıları, geometri alanındaki temel kavramlardan biridir. Bu yazıda, üçgenlerin iç açılarıyla ilgili önemli kurallar, açıların büyüklüğü, dış açı ilişkileri ve kenarlarla olan bağlantıları ele alınarak, üçgenlerin özelliklerini anlamaya yönelik bilgiler sunulmaktadır.
Üçgenin İç Açıları Kuralları Üçgen, üç kenarı ve üç açısı olan temel bir geometrik şekildir. Üçgenlerin iç açıları, geometri alanında önemli bir yere sahiptir. Bu iç açılar, üçgenin özelliklerini anlamak ve çeşitli geometrik problemleri çözmek için kritik öneme sahiptir. Bu makalede, üçgenin iç açılarıyla ilgili temel kurallar ve özellikler ele alınacaktır. 1. Üçgenin İç Açıları Toplamı Her üçgenin iç açıları toplamı her zaman 180 derecedir. Bu kurala göre, bir üçgenin iç açıları A, B ve C olarak adlandırılırsa, aşağıdaki eşitlik geçerlidir:
Bu kural, tüm üçgenler için geçerli olup, üçgenin şekli veya boyutuyla ilgili herhangi bir bağımlılık göstermez. 2. Açıların Büyüklüğü Üçgenin iç açıları arasındaki ilişki, üçgenin türüne göre değişiklik gösterebilir. Üçgenlerin türleri, açı genişliklerine göre sınıflandırılabilir:
Bu açı ilişkileri, üçgenin belirli özelliklerini ve kullanım alanlarını etkileyebilir. 3. Açı Çiftleri ve Dış Açı Kuralları Üçgenin bir kenarını uzattığımızda, dış açılar oluşur. Dış açılar, üçgenin iç açıları ile ilişkilidir. Bir üçgenin dış açısı, ona komşu olan iki iç açının toplamına eşittir. Bu ilişki aşağıdaki gibi ifade edilebilir:
Bu kural, geometrik problemlerin çözümünde sıklıkla kullanılmaktadır. 4. Üçgenin Açı Ortayları Üçgenin iç açıları, üçgenin açı ortayları kullanılarak da incelenebilir. Açı ortayı, üçgenin bir iç açısını iki eşit parçaya bölen bir doğru parçası olarak tanımlayabiliriz. Açı ortayların kesişim noktası, üçgenin iç açılarının büyüklükleri ile ilgili önemli bilgiler sağlar ve aynı zamanda üçgenin iç merkezini oluşturur. 5. Üçgenin İç Açıları ile Üçgenin Kenarları Arasındaki İlişki Üçgenin iç açıları, aynı zamanda üçgenin kenarları ile de ilişkilidir. Örneğin, bir üçgenin daha uzun kenarına karşılık gelen iç açı, daha büyük olurken; daha kısa kenarına karşılık gelen iç açı daha küçük olmaktadır. Bu ilişki, üçgenin kenar uzunlukları ile açıları arasındaki temel bir bağıntıdır. Ek Bilgiler |
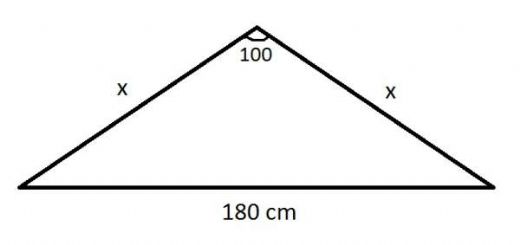















































Üçgenin iç açıları kuralları, geometri derslerinde öğrendiğim en önemli konulardan biri. 180 derecelik toplam, üçgenin temel özelliklerini anlamamı sağlıyor. Ayrıca, açıların büyüklüğü ile kenar uzunlukları arasındaki ilişki de oldukça ilginç. Bu kurallar, geometrik problemleri çözmemde bana büyük yardımcı oluyor.
Merhaba Sami,
Üçgenin iç açıları ve bu açıların toplamı gerçekten de geometri derslerinin temel taşlarından biridir. 180 Derece Kuralı sayesinde üçgenin yapısını daha iyi kavrayabiliyoruz. Bu bilgi, üçgenin kenar uzunlukları ile açılar arasındaki ilişkiyi anlamamıza yardımcı oluyor; bu da çeşitli geometrik problemleri çözmemizi kolaylaştırıyor. Açı-Kenar İlişkisi ise geometri dünyasında önemli bir yere sahiptir ve birçok farklı problemde kullanılabilir. Geometriye olan ilginizin bu kurallarla daha da derinleşeceğine eminim. Başarılar dilerim!
Üçgenin iç açıları toplamı her zaman 180 derece olarak bilinir. Bu kural, farklı türdeki üçgenlerin özelliklerini anlamak için kritik bir öneme sahiptir. Üçgenin iç açıları arasındaki ilişkiyi bilmek, geometri problemlerinde önemli bir avantaj sağlar.
Değerli Mevlüt,
Üçgenlerin iç açıları toplamının her zaman 180 derece olduğu bilgisi, geometri açısından gerçekten de temel bir kuraldır. Bu kural, üçgenlerin farklı türleri arasında ilişki kurmamıza olanak tanır. Örneğin, eşkenar üçgenlerde tüm açıların eşit olduğunu bilmek, problemlerde daha hızlı çözümler bulmamıza yardımcı olabilir. Ayrıca, üçgenin iç açıları arasındaki ilişki, çokgenler ve diğer geometrik şekillerle bağlantılı olarak da geniş bir perspektif sunar. Geometri sorunlarını çözmek için bu temel bilgiyi kullanmak, analitik düşünme yeteneğimizi geliştirmektedir. Bu nedenle, üçgenin iç açıları hakkında bilgi sahibi olmak, matematiksel düşünceyi ilerletmek adına oldukça değerlidir.
Saygılarımla,
Üçgenin iç açıları kuralları hakkında daha fazla bilgi edinmek istiyorum. Özellikle iç açı bulma formülü nasıl uygulanır? Üçgenin türüne göre bu formül değişir mi? Eğer bu konuda deneyimlerinizi paylaşırsanız, daha iyi anlayabilirim. Teşekkürler!
Üçgenin İç Açılarının Kuralları
Üçgenin iç açılarının toplamı her zaman 180 derece olarak bilinir. Bu, üçgenin herhangi bir türü için geçerlidir. Yani, ister dik üçgen, ister dar üçgen, isterse geniş üçgen olsun, iç açılarının toplamı 180 derecedir.
İç Açı Bulma Formülü
Üçgenin iç açılarını bulmak için, eğer iki açı verilmişse, üçüncü açıyı bulmak için şu formülü kullanabilirsiniz:
Üçüncü açı = 180 - (Birinci açı + İkinci açı)
Örneğin, bir üçgende bir açının 50 derece, diğer açının ise 70 derece olduğunu varsayalım. Üçüncü açıyı bulmak için:
Üçüncü açı = 180 - (50 + 70) = 180 - 120 = 60 derece
Üçgen Türlerine Göre Değişiklik
Üçgen türlerine göre iç açıların özellikleri değişmez; fakat açıların büyüklükleri türüne göre farklılık gösterebilir. Örneğin:
- Dik Üçgen: Bir açısı 90 derece olan üçgendir.
- Dar Üçgen: Tüm açıları 90 dereceden küçük olan üçgendir.
- Geniş Üçgen: Bir açısı 90 dereceden büyük olan üçgendir.
Her üçgen türünde de iç açıların toplamı 180 derece olma kuralı geçerlidir.
Umarım bu bilgiler, iç açılar ve formüller hakkında daha iyi bir anlayış sağlar. Başka sorularınız olursa memnuniyetle cevaplarım. Teşekkürler!
Üçgenin iç açılarının toplamının her zaman 180 derece olduğunu biliyor muydun? Bu, geometri derslerinde sıkça karşımıza çıkan bir kural. Üçgenin türleri arasında eşkenar, ikizkenar ve çeşitkenar üçgenler bulunuyor. Eşkenar üçgenin tüm kenarları eşit ve iç açıları 60 derece, ikizkenar üçgende ise iki kenar eşit ve bu kenarların karşısındaki açı da eşit. Peki, sen üçgenlerle ilgili bu özellikleri ne kadar iyi biliyorsun?
Muaddal,
Üçgenin İç Açıları hakkında verdiğin bilgi oldukça doğru. Gerçekten de bir üçgenin iç açıları toplamı her zaman 180 derece eder. Bu, geometri temel kavramlarından biridir ve üçgenlerle ilgili birçok problemde önemli bir rol oynar.
Üçgen Türleri konusuna gelince, eşkenar, ikizkenar ve çeşitkenar üçgenler arasındaki farklılıklar oldukça ilginçtir. Eşkenar üçgende tüm kenarlar ve açıların eşit olduğunu belirtmen önemli; bu, simetrik bir yapı oluşturur. İkizkenar üçgende ise iki kenarın eşit olması, geometrik şeklin farklı bir estetik sunmasını sağlar.
Üçgen Özellikleri açısından eklemek gerekirse, üçgenlerin iç açıları dışında dış açıları da vardır ve bir dış açının, karşısındaki iki iç açının toplamına eşit olduğunu bilmek de faydalıdır. Üçgenlerle ilgili bu tür temel bilgileri öğrenmek, daha karmaşık geometri konularında ilerlemen için sağlam bir temel oluşturur.
Senin üçgenlerle ilgili bilgini geliştirmek adına, üçgenlerin alan hesaplamaları veya Pythagor teoremi gibi konulara da yönelmeni öneririm. Bu şekilde, geometrik kavramları daha kapsamlı bir şekilde anlayabilirsin.