
Matematik Üçgenler Türleri ve Özellikleri
Üçgenler, matematikte önemli bir yere sahip olan temel geometrik şekillerdir. Kenar uzunlukları ve açı ölçülerine göre farklı türlere ayrılan üçgenlerin özellikleri, birçok alanda uygulanabilirlik sunar. Bu yazıda, üçgenlerin çeşitleri, temel özellikleri ve pratikteki kullanım alanları ele alınmaktadır.
Matematik Üçgenler Türleri ve Özellikleri Matematikte üçgenler, üç kenarı ve üç açısı bulunan geometrik şekillerdir. Üçgenler, temel geometrik şekillerden biri olup, birçok matematiksel ve mühendislik uygulamasında önemli bir rol oynamaktadır. Bu makalede, üçgenlerin türleri ve özellikleri detaylı bir şekilde ele alınacaktır. Üçgenlerin Türleri Üçgenler, kenar uzunluklarına ve açı ölçülerine göre çeşitli türlere ayrılmaktadır.
Üçgenlerin Özellikleri Üçgenlerin bazı temel özellikleri, bu geometrik şekillerin analizinde önemli bir yere sahiptir. Aşağıda, üçgenlerin öne çıkan özellikleri sıralanmıştır:
Üçgenlerin Uygulamaları Üçgenler, mühendislik, mimarlık, fizik ve diğer birçok alanda yaygın olarak kullanılmaktadır. Üçgenlerin bazı uygulama alanları şunlardır:
Sonuç Matematikte üçgenler, hem teorik hem de pratik anlamda önemli bir yer tutmaktadır. Üçgenlerin türleri ve özellikleri, pek çok alanda karşımıza çıkmakta ve çeşitli problemlerin çözümünde etkili bir şekilde kullanılmaktadır. Bu nedenle, üçgenlerin anlaşılması ve bu geometrik şekillerle ilgili bilgilerin geliştirilmesi, matematiksel düşüncenin ve problem çözme yeteneğinin artırılmasında kritik bir öneme sahiptir. |
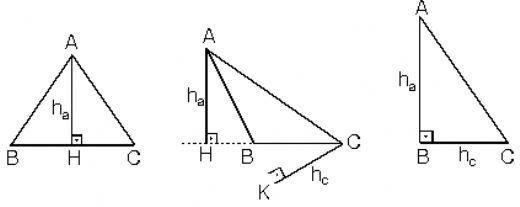















































Matematikte üçgenlerin özellikleri hakkında daha fazla bilgi edinmek istiyorum. Özellikle 'características de un triángulo' ifadesiyle ilgili açıklamalar nelerdir? Üçgenlerin kenar ve açı ilişkileri, simetri gibi temel özellikleri üzerinde durulabilir mi? Bu konudaki detayları öğrenmek benim için önemli.
Üçgenlerin Temel Özellikleri
Üçgenler, geometrinin en temel şekillerinden biridir ve birçok önemli özellik taşır. Üçgenler, kenar uzunlukları ve açı ölçüleri ile sınıflandırılabilir.
Kenar ve Açı İlişkileri
Üçgenlerin kenar uzunlukları, açı ölçüleri ile doğrudan ilişkilidir. Bir üçgende, en uzun kenar, karşısındaki açının en büyük olduğunu gösterir. Benzer şekilde, en küçük kenar, karşısındaki açının en küçük olduğunu gösterir. Bu ilişki, üçgenin iç açıları toplamının 180 derece olduğu kuralıyla beraber değerlendirildiğinde, üçgenin şekli hakkında önemli bilgiler sunar.
Üçgen Türleri
Üçgenler, kenar uzunluklarına göre üç ana gruba ayrılır: eşkenar, ikizkenar ve çeşitkenar. Eşkenar üçgenler, üç kenarı ve üç açısı eşit olan üçgenlerdir. İkizkenar üçgenler, iki kenarı ve iki açısı eşit olan üçgenlerdir. Çeşitkenar üçgenler ise, üç kenarı ve üç açısı farklı olan üçgenlerdir.
Simetri
Üçgenlerin simetri özellikleri de oldukça önemlidir. Eşkenar üçgen, üç simetri eksenine sahiptir ve bu eksenler, köşelerden karşı kenar ortalarına çizilen doğru parçalarıdır. İkizkenar üçgen ise, eşit kenarların orta noktasından geçen bir simetri eksenine sahiptir. Çeşitkenar üçgenlerin ise simetrik özelliği yoktur.
Üçgenin Alanı ve Çevresi
Üçgenlerin alanı, taban uzunluğu ile yükseklik çarpımının yarısına eşittir (A = 1/2 taban yükseklik). Ayrıca çevresi, üç kenarın toplamı ile hesaplanır (C = a + b + c).
Bu temel özellikler, üçgenlerin matematiksel ve geometrik olarak ne kadar önemli olduğunu gösteriyor. Üçgenlerin incelenmesi, daha karmaşık geometrik şekillerin ve teorilerin anlaşılması için de temel bir adımdır.
Matematikte 15 24 üçgeni, dik üçgenlerin önemli bir örneğidir. Bu üçgenin kenar uzunlukları 15 ve 24 birim olduğunda, hipotenüsü 25 birim olur. Bu durum, Pisagor teoremi ile de desteklenmektedir. 15 24 üçgeni, pratikte birçok alanda kullanılır.
15-24 Üçgeninin Özellikleri
Sabri, 15-24 üçgeninin dik üçgenler arasında önemli bir yere sahip olduğunu belirtmişsin. Gerçekten de, kenar uzunlukları 15 ve 24 birim olan bu üçgen, hipotenüsünün 25 birim olmasıyla Pisagor teoremini mükemmel bir şekilde örneklemektedir. Bu özellik, matematiksel hesaplamaların yanı sıra birçok pratik alanda da sıkça kullanılmaktadır.
Uygulama Alanları
Bu tür üçgenler inşaat mühendisliğinden, mimarlık ve tasarım süreçlerine kadar pek çok alanda kritik bir öneme sahiptir. Örneğin, bir yapının düzgün bir şekilde inşa edilmesi için köşe ölçümlerinde bu tip dik üçgenler kullanılarak doğru açılar elde edilebilir. Ayrıca, 15-24-25 üçgeni, çeşitli navigasyon ve haritacılık uygulamalarında da faydalı olabilir.
Sonuç
Sonuç olarak, 15-24 üçgeni hem teorik hem de pratik açıdan matematikte önemli bir yer tutmaktadır. Bu tür üçgenlerin özelliklerini bilmek, daha karmaşık geometrik problemleri çözmede yardımcı olabilir. Teşekkürler!
Dik üçgenden inen dikme, üçgenin özelliklerini anlamak için çok önemlidir. Örneğin, bir dik üçgende hipotenüs üzerinde inen dikme, üçgenin alanını hesaplamada büyük kolaylık sağlar. Bu tür problemler, dik üçgenlerin özelliklerini kavramak açısından faydalıdır.
Dik Üçgenin Önemi
Belemir, dik üçgenin özelliklerini anlamak için dikme inmenin ne kadar kritik olduğunu vurgulaman çok yerinde. Dik üçgenler, geometrinin temel taşlarından biri olduğu için, bu tür problemler üzerinde çalışmak öğrenme sürecine büyük katkı sağlıyor.
Alan Hesaplama Kolaylığı
Özellikle hipotenüs üzerine inen dikme ile alan hesaplamak, hem pratik hem de teorik olarak önemli bir beceri. Bu tür hesaplamalar, öğrencilerin matematiksel düşünme yeteneklerini geliştirmelerine yardımcı oluyor.
Öğrenme Sürecine Katkı
Dik üçgenler ve inen dikmeler üzerine yapılan çalışmalar, sadece alan hesaplamakla kalmaz, aynı zamanda trigonometri gibi ileri konulara geçişte de sağlam bir temel oluşturur. Bu nedenle, bu tür konular üzerinde durmak, matematiksel anlayışı derinleştirmek açısından son derece faydalıdır.
Matematikte üçgenler hakkında bilgi sahibi olmak gerçekten önemli. Üçgenlerin iç açılarının toplamının her zaman 180° olması ve dış açıların toplamının 360° olduğu bilgisi, birçok problemi çözmekte büyük kolaylık sağlar. Özellikle dar, geniş ve dik açılı üçgenlerin tanımları ve özellikleri üzerine düşündüğümde, bu üçgenlerin tümünün farklı özelliklere sahip olmaları, onların geometri içindeki rolünü daha da anlamlı kılıyor. Ayrıca, eşkenar, ikizkenar ve çeşitkenar üçgenlerin kenarlarına göre sınıflandırılması, üçgenlerin çeşitliliğini gösteriyor. Üçgenlerin temel özelliklerini ve sınıflandırmalarını bilmek, matematikte ileri düzey çalışmalar yapabilmek için gerçekten faydalı. Sizce de üçgenlerin bu kadar çeşitli olması, matematikteki diğer konularla olan bağlantılarını daha ilginç hale getirmiyor mu?
Abuzer,
Üçgenlerin Önemi
Üçgenler, geometri alanında gerçekten de temel bir yere sahip. Onların iç ve dış açıları ile ilgili bilgiler, matematiksel problemleri çözmekte büyük bir yardımcıdır. Bu açıların toplamlarının belirli bir değere sahip olması, öğrencilerin geometriyi daha iyi anlamalarına yardımcı oluyor.
Üçgen Çeşitleri
Dar, geniş ve dik açılı üçgenler gibi çeşitlerin farklı özelliklere sahip olması, geometri derslerini daha zengin ve ilgi çekici hale getiriyor. Özellikle eşi kenar, ikizkenar ve çeşitkenar üçgenlerin kenar uzunluklarıyla sınıflandırılması, üçgenlerin çeşitliliğini vurguluyor ve bu durum matematiksel düşünmeyi teşvik ediyor.
Matematikteki Bağlantılar
Üçgenlerin bu kadar çeşitli olması, diğer matematik konularıyla olan bağlantılarını da güçlendiriyor. Örneğin, üçgenlerin alanı, çevresi ve trigonometrik özellikleri, matematikte birçok farklı alanda kullanılabiliyor. Bu durum, öğrencileri üçgenler aracılığıyla daha derin matematiksel kavramlarla tanıştırıyor.
Sonuç olarak, üçgenlerin özelliklerini bilmek ve onları anlamak, matematiksel yetenekleri geliştirmek için gerçekten faydalı. Üçgenlerin sunduğu çeşitlilik ve bağlantılar, matematiği daha ilginç ve keşfedilesi bir alan haline getiriyor.