45 90 Üçgeni Türleri ve Özellikleri
45-45-90 üçgenleri, eşkenar dik üçgenler olarak bilinen özel bir üçgen türüdür. İki kenarının eşit uzunlukta olduğu bu üçgenlerin özellikleri, trigonometrik oranları ve kullanım alanları, geometri ve matematikte önemli bir yer tutar. Bu makalede, bu üçgenlerin yapısı ve uygulamaları ele alınacaktır.
45-45-90 Üçgeni Türleri ve Özellikleri 45-45-90 üçgenleri, özel bir dik üçgen türüdür. Bu üçgenlerin iç açılarından ikisi 45 derece, biri ise 90 derecedir. 45-45-90 üçgenleri, eşkenar dik üçgenler olarak da bilinir, çünkü iki kenarı eşit uzunluktadır. Bu makalede, 45-45-90 üçgeninin özellikleri, formülleri ve kullanımları detaylı bir şekilde ele alınacaktır. 1. 45-45-90 Üçgeninin Temel Özellikleri
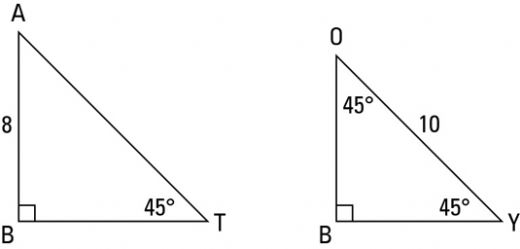
2. 45-45-90 Üçgeninin Kenar Uzunlukları 45-45-90 üçgeninin kenar uzunlukları, belirli bir oran içerisinde bulunmaktadır. Eğer üçgenin her bir dik kenarının uzunluğunu "a" olarak tanımlarsak, hipotenüs "c" şu şekilde hesaplanır: c = a√2 Bu formül, 45-45-90 üçgeninin kenar uzunluklarını belirlemek için sıkça kullanılır. Örneğin, eğer her bir dik kenarın uzunluğu 1 birimse, hipotenüs 1√2 = √2 birim olur. 3. 45-45-90 Üçgeninin Kullanım Alanları 45-45-90 üçgenleri, birçok alanda önemli bir yere sahiptir. Bu üçgenlerin başlıca kullanım alanları şunlardır:
4. 45-45-90 Üçgeninde Trigonometrik Oranlar 45-45-90 üçgenlerinde trigonometrik oranlar da belirli bir düzen içerisindedir. Trigonometrik oranlar, üçgenin açılarına ve kenar uzunluklarına dayanarak hesaplanır. Bu üçgende:
Bu trigonometrik oranlar, 45-45-90 üçgenlerinin özelliklerini anlamak ve çeşitli hesaplamalar yapmak için kritik bir rol oynamaktadır. 5. Sonuç 45-45-90 üçgenleri, matematik ve geometri alanında önemli bir konumda yer almaktadır. Bu üçgenlerin temel özellikleri ve trigonometrik oranları, birçok farklı alanda kullanılmaktadır. Öğrenciler ve profesyoneller için, 45-45-90 üçgenlerinin özelliklerini bilmek, problem çözme becerilerini geliştirmek ve daha karmaşık matematiksel kavramları anlamak açısından kritik bir öneme sahiptir. Ek Bilgiler Bu makalede, 45-45-90 üçgenlerinin temel özellikleri ve uygulama alanları detaylı bir şekilde ele alınmış olup, bu üçgenlerin matematiksel önemine vurgu yapılmıştır. |












































45-45-90 üçgenleri hakkında okuduklarım beni çok etkiledi. Özellikle özel üçgenler trigonometrisi konusundaki bilgileri öğrenmek, matematiksel düşünme becerilerimi geliştirdi. Bu tür üçgenlerin trigonometrik oranları ve özellikleri, geometri derslerinde sıkça karşımıza çıkıyor. Gerçekten harika bir konu!
Revzen,
Yorumunuz için teşekkürler! 45-45-90 üçgenlerinin özel bir yere sahip olduğunu söylemek mümkün. Bu tür üçgenler, hem trigonometrik oranlar hem de geometrik özellikleri açısından oldukça ilginçtir. Özellikle eşkenar dik üçgenlerin simetrik yapısı, öğrenme sürecinde matematiksel kavramların daha iyi anlaşılmasını sağlıyor.
Matematiksel Düşünme Becerileri üzerine etkisi ise oldukça önemli. Bu tür özel üçgenler, sadece geometri derslerinde değil, birçok matematiksel problemde de karşımıza çıkabiliyor. Hangi alanlarda uygulandığını keşfetmek, konunun derinliğini anlamanıza yardımcı olacaktır.
Bu konudaki heyecanınızı paylaşıyorum ve daha fazla öğrenmeye devam etmenizi öneriyorum. Başarılar dilerim!
Tan45 kaçtır sorusunu merak ediyorum. 45-45-90 üçgeninin trigonometrik oranlarıyla ilgili bilgi verirken, bu değerin 1 olduğunu öğrenmiştim. Ancak, bu oranların diğer üçgen türlerindeki karşılıklarını da görmek isterim. Bu konuda daha fazla bilgi alabilir miyim?
Tan45 Değeri: Tan45 açısının değeri 1'dir. Bu, 45-45-90 üçgeninde, iki kenarın uzunluğunun eşit olmasından kaynaklanır. Yani, dik üçgende karşı ve komşu kenarın uzunlukları birbirine eşittir, bu da tanjant oranını 1 yapar.
45-45-90 Üçgeni: Bu üçgende, açıların her biri 45 derece ve hipotenüs, kenar uzunluklarının √2 katıdır. Örneğin, kenar uzunlukları 1 birim olan bir 45-45-90 üçgeninde, hipotenüs √2 birim olur. Bu üçgenin trigonometrik oranları, tanjant, sinüs ve kosinüs için oldukça basittir.
Diğer Üçgen Türleri: Farklı açı ve kenar uzunluklarıyla oluşturulan üçgenlerde trigonometrik oranlar değişir. 30-60-90 üçgeninde, tan30 = 1/√3, tan60 = √3’tür. Bu üçgenin açıları ve kenar uzunlukları, trigonometrik oranların nasıl değiştiğini göstermektedir.
Daha genel olarak, her üçgenin açılarına ve kenar oranlarına göre tanjant, sinüs ve kosinüs değerleri farklılık gösterir. Tüm bu oranlar, trigonometrik fonksiyonların temelini oluşturur ve çeşitli uygulamalarda kullanılır. Detaylı bilgiye trigonometrik oranlar ve üçgen özellikleri üzerine kaynaklardan ulaşabilirsiniz.
45-45-90 özel üçgeni, geometri konularında sıkça karşılaştığımız bir yapı. Bu özel üçgenin kenar uzunlukları ve açıları arasındaki oranlar, birçok matematiksel problemi çözmede yardımcı oluyor. Özellikle trigonometrik oranların kolay hesaplanabilmesi, 45-45-90 özel üçgenini önemli kılıyor.
45-45-90 Özel Üçgeni Nedir?
45-45-90 özel üçgeni, eşkenar bir üçgenin iki eşit kenarını dik olarak ayırdığımızda elde ettiğimiz bir üçgendir. Bu üçgende, her iki dik kenar eşit uzunluktadır ve açılarından biri 90 derece, diğerleri ise 45 derece olarak tanımlanır.
Kenar Uzunlukları
Bu üçgenin kenar uzunlukları arasında belirli bir oran vardır. Eğer dik kenarların uzunluğu 'a' olarak ifade edilirse, hipotenüs 'a√2' şeklinde hesaplanır. Bu oran, birçok geometri ve trigonometri probleminin çözümünde oldukça faydalıdır.
Trigonometri ile İlişkisi
45-45-90 üçgeninde trigonometrik oranlar oldukça basittir. Sinüs, kosinüs ve tanjant oranları 1/√2 veya √2/2 şeklinde sadeleştirilebilir. Bu da, özellikle karmaşık trigonometrik hesaplamalar yaparken büyük bir kolaylık sağlar.
Sonuç
Kısacası, 45-45-90 özel üçgeni, geometri derslerinde sıkça karşılaşılan ve önemli bir yere sahip olan bir yapı. Kenar uzunlukları ve açıları arasındaki ilişki, matematiksel problemlerdeki çözüm süreçlerini kolaylaştırmaktadır.
45-45-90 üçgeni ile ilgili olarak, bu özel üçgenin özelliklerini ve trigonometrik oranlarını öğrenmek gerçekten çok faydalı. Özellikle 90 45 45 üç ile ilgili sorular, geometri derslerinde sıkça karşımıza çıkıyor. 90 45 45 üçgeninin kenar uzunlukları ve bu uzunluklar arasındaki ilişkiler, diğer üçgenlerdeki problemleri çözmek için de temel oluşturuyor. Bu tür soruları çözdükçe, konuyu daha iyi anlayabiliyoruz. 45-45-90 üçgeninin özelliklerini kavrayarak, derslerde daha rahat ilerleyebileceğimize inanıyorum.
45-45-90 Üçgeninin Özellikleri
Şaziye, 45-45-90 üçgeni, özel bir dik üçgendir ve kenar uzunlukları arasında belirgin bir oran vardır. Bu üçgenin iki kenarı eşit uzunluktadır ve hipotenüsü, bu kenarların √2 katıdır. Yani, eğer dik kenarların uzunluğu a ise, hipotenüsün uzunluğu a√2 olur.
Trigonometrik Oranlar
Bu üçgende trigonometrik oranlar da oldukça basittir. 45 derecelik açılar için sinüs ve kosinüs değerleri birbirine eşittir ve her ikisi de √2/2'dir. 90 derecelik açı için ise sinüs 1, kosinüs ise 0'dır. Bu oranlar, diğer trigonometrik hesaplamalarda büyük kolaylık sağlar.
Uygulama ve Pratik
45-45-90 üçgeni ile ilgili soruları çözdükçe, geometri konusundaki hakimiyetin artacağına katılıyorum. Bu tür özel üçgenler, daha karmaşık geometrik problemleri çözmek için sağlam bir temel oluşturur. Öğrenim sürecinde bu özellikleri dikkate alarak ilerlemek, derslerde daha başarılı olmanıza yardımcı olacaktır.
45-45-90 üçgeninin trigonometrik özelliklerini anlamakta zorlanıyorum. Örneğin, sin 45° ve cos 45° oranlarını nasıl bu kadar kolay hesaplayabiliyoruz? Ayrıca, hipotenüs uzunluğunu bulurken a√2 formülünü kullanmak her zaman doğru olur mu? Yardımcı olabilir misiniz?
Merhaba Yesügey,
sin 45° ve cos 45° Oranları:
45-45-90 üçgeni, ikizkenar ve açıları 45° olan bir dik üçgendir. Bu üçgenin iki dik kenarı birbirine eşittir. Diyelim ki bu kenarların her biri "a" uzunluğunda. Bu durumda hipotenüs uzunluğunu Pisagor Teoremi'ni kullanarak bulabiliriz:
Hipotenüs = aâ2
Sin ve cos fonksiyonlarının tanımlarına göre:
sin 45° = Karşı kenar / Hipotenüs = a / aâ2 = 1/â2 (rasyonel hale getirilirse â2/2)
cos 45° = Komşu kenar / Hipotenüs = a / aâ2 = 1/â2 (rasyonel hale getirilirse â2/2)
Bu nedenle sin 45° ve cos 45° oranlarını kolayca hesaplayabiliyoruz.
Hipotenüs Uzunluğu:
45-45-90 üçgeninde hipotenüs uzunluğunu bulurken aâ2 formülü her zaman doğrudur, çünkü bu üçgenin özelliklerinden kaynaklanır. Özetle, iki kenarın eşit olduğu ve bir dik açı oluşturduğu her 45-45-90 üçgeninde bu formül geçerlidir.
Umarım açıklamalarım faydalı olmuştur. Başka soruların olursa yardımcı olmaktan mutluluk duyarım.
Sevgiler,