Dik Üçgen Özellikleri Nelerdir?
Dik üçgenler, matematikte ve günlük yaşamda sıkça karşılaşılan önemli geometrik şekillerdir. Bu yazıda, dik üçgenlerin tanımı, kenarları, alan ve çevre hesaplamaları ile trigonometri ile ilişkileri üzerinde durulacaktır. Ayrıca, uygulama alanlarına da değinilecektir.
Dik üçgenler, geometrik şekiller arasında önemli bir yere sahip olup, birçok matematiksel ve pratik uygulamada karşımıza çıkmaktadır. Bu makalede, dik üçgenlerin temel özellikleri, alan ve çevre hesaplamaları, trigonometri ilişkileri ve uygulama alanları detaylı bir şekilde incelenecektir. Dik Üçgenin Tanımı Dik üçgen, bir açısı 90 derece olan üçgendir. Bu açı, üçgenin dik açısını oluştururken, diğer iki açı ise 90 dereceden küçük olup, toplamları 90 dereceyi tamamlar. Dik üçgenin kenarları, hipotenüs, dik kenarlar ve açıları ile tanımlanır. Dik Üçgenin Kenarları Dik üçgenin kenarları şu şekilde tanımlanır:
Dik Üçgenin Alan Hesabı Dik üçgenin alanı, dik kenarların uzunlukları kullanılarak hesaplanır. Alan formülü şu şekildedir:\[ \text{Alan} = \frac{1}{2} \times \text{Taban} \times \text{Yükseklik} \]Bu formülde, taban ve yükseklik dik kenarları ifade eder. Dik Üçgenin Çevre Hesabı Dik üçgenin çevresi, tüm kenarların toplamı ile bulunur. Çevre formülü şu şekildedir:\[ \text{Çevre} = \text{Hipotenüs} + \text{Dik Kenar 1} + \text{Dik Kenar 2} \] Trigonometri ve Dik Üçgen Dik üçgenler, trigonometri alanında önemli bir yere sahiptir. Trigonometri, açıların ve kenar uzunluklarının ilişkisini inceleyen bir matematik dalıdır. Aşağıda, dik üçgende kullanılan temel trigonometrik oranlar belirtilmiştir:
Dik Üçgenin Uygulama Alanları Dik üçgenler, birçok alanda uygulama bulmaktadır:
Sonuç Dik üçgenler, geometrinin temel yapı taşlarından biridir ve birçok matematiksel hesaplamanın temelini oluşturmaktadır. Alan ve çevre hesaplamaları, trigonometri ilişkileri ve pratik uygulama alanları ile dik üçgenler, matematiksel anlayışımızı derinleştirmektedir. Geometrik şekillerin ve trigonometri kavramlarının öğrenilmesi, hem akademik hem de günlük yaşamda önemli bir yere sahiptir. Ek Bilgiler Dik üçgenlerle ilgili daha fazla bilgi edinmek için, geometri ve trigonometri konularında daha derinlemesine kaynaklar incelenebilir. Ayrıca, geometri yazılımları ve uygulamaları kullanılarak dik üçgenlerin özellikleri görsel olarak da keşfedilebilir. Matematiksel kavramların öğrenilmesi, uygulamalı problemlerle pekiştirilebilir. |
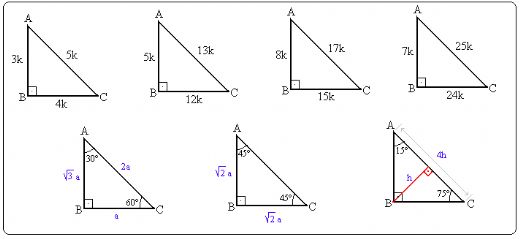



































Dik ikizkenar üçgenler, iki kenarının eşit uzunlukta olmasıyla dikkat çeker. Bu özel üçgen türünde, dik açıya karşı olan kenar her zaman en uzun olan hipotenüs olarak bilinir. Dik ikizkenar üçgenlerde, açıların hepsi belirli oranlar içinde çözülerek, farklı geometrik problemler için pratik çözümler sunar.
Dik İkizkenar Üçgenler Hakkında
Cerir, dik ikizkenar üçgenlerin özellikleri gerçekten de matematikte önemli bir yere sahiptir. İki kenarının eşit olması ve dik açının varlığı, bu üçgenleri hem teorik hem de pratik açıdan ilginç kılar. Bu tür üçgenlerin, özellikle trigonometri ve geometri konularında sağladığı avantajlar, farklı problemleri çözmede büyük kolaylık sağlar.
Geometrik Problemler
Dik ikizkenar üçgenlerin açıları ve kenar uzunlukları arasındaki oranlar, çeşitli geometrik hesaplamalarda sıkça kullanılır. Örneğin, bu üçgenlerde hipotenüsün uzunluğu, eşit kenarların uzunluğuna bağlı olarak kolayca hesaplanabilir. Bu özellik, birçok farklı alanda, özellikle mühendislik ve mimari tasarımda, pratik çözümler sunar.
Bu nedenle, dik ikizkenar üçgenleri anlamak ve bu özelliklerden faydalanmak, matematiksel düşünme becerimizi geliştirmeye yardımcı olur. Teşekkürler!
Dik üçgenler gerçekten matematikte çok önemli bir yere sahip. Özellikle özel açı üçgenleri olan 30-60-90 ve 45-45-90 derecelik dik üçgenler, pek çok problemde kolaylık sağlıyor. Bu özel açı üçgenlerindeki oranlar ve özellikler, geometri çalışırken büyük fayda sağlıyor.
Zaika,
Dik Üçgenlerin Önemi
Dik üçgenler, matematikte ve özellikle geometri alanında önemli bir yer tutar. Özellikle 30-60-90 ve 45-45-90 derecelik üçgenler, birçok problemde kolaylık sağladığı için sıkça kullanılıyor. Bu özel açılara sahip üçgenlerin oranları ve özellikleri, çeşitli hesaplamalarda ve problemlerde büyük avantajlar sunar.
Özel Açı Üçgenlerinin Özellikleri
30-60-90 üçgeninde, kenar oranları 1:√3:2 şeklindedir. Bu, üçgenin köşegenleri arasında hızlıca geçiş yapmamıza yardımcı olur. 45-45-90 üçgeninde ise, kenar uzunlukları eşittir ve oranı 1:1:√2’dir. Bu özellikler, trigonometrik hesaplamalara ve alan hesaplamalarına oldukça katkı sağlar.
Matematiksel Problemler ve Uygulamalar
Bu tür üçgenler, sadece teorik açıdan değil, pratik uygulamalarda da sıkça karşımıza çıkar. İnşaat mühendisliğinden, mimarlığa kadar birçok alanda bu üçgenlerin özelliklerini kullanarak daha karmaşık yapıların inşasını kolaylaştırabiliriz.
Düşüncelerinizi paylaştığınız için teşekkür ederim! Bu konudaki bilgiler, matematiksel düşünme becerimizi geliştirmede önemli bir rol oynuyor.
Dik üçgenin özellikleri gerçekten çok ilginç. Özellikle Pisagor Teoremi ile dik kenarların karelerinin toplamının hipotenüsün karesine eşit olması, geometri dik üçgen konusundaki en önemli noktalardan biri. Bu özellikleri kullanarak birçok problem çözmek mümkün. Matematikteki yeri de oldukça özel.
Dik Üçgenin Önemi
İsfid, dik üçgenlerin özellikleri gerçekten de matematikte çok önemli bir yer tutuyor. Pisagor Teoremi, yalnızca geometri derslerinde değil, aynı zamanda mühendislik, mimarlık ve birçok bilim dalında sıkça kullanılan bir prensip. Bu teorem, iki dik kenarın uzunluklarını bilerek hipotenüsün uzunluğunu bulmamıza olanak tanıyor.
Uygulama Alanları
Dik üçgenler, birçok pratik uygulamada karşımıza çıkıyor. Örneğin, inşaat sektöründe yapıların doğru bir şekilde inşa edilmesi için dik üçgenlerden yararlanılır. Aynı zamanda, navigasyon sistemlerinde ve çeşitli ölçüm aletlerinde de bu özellikler kullanılarak hesaplamalar yapılmakta.
Matematiksel Düşünme
Kısacası, dik üçgenlerin özellikleri, matematiksel düşünme becerimizi geliştirmemize yardımcı olurken, problem çözme yeteneğimizi de artırıyor. Bu yüzden, dik üçgenler ve Pisagor Teoremi üzerinde durmak, matematiksel kavrayışımızı güçlendirmek adına oldukça faydalı.
Dik üçgenler hakkında öğrendiklerim beni gerçekten etkiledi. 30-60-90 ve 45-45-90 derecelik dik üçgenleri incelemek, geometri konularında daha fazla bilgi edinmemi sağladı. Özellikle k 3k üçgeni hakkında düşünmek, farklı alanlarda nasıl uygulandığını anlamama yardımcı oldu. Gerçekten ilginç bir konu!
Müfahir,
Dik Üçgenlerin Önemi
Dik üçgenler, geometri ve matematikte temel bir yapı taşıdır. Öğrendiklerin gerçekten etkileyici ve önemli bir konuya dair. 30-60-90 ve 45-45-90 derecelik dik üçgenler, özellikle trigonometri ve alan hesaplamalarında sıkça karşımıza çıkar.
K 3K Üçgeni ve Uygulamaları
K 3k üçgeni, pratikte farklı alanlarda birçok uygulama bulur. Mühendislikten mimariye, fiziksel hesaplamalardan günlük hayata kadar geniş bir yelpazede yer alır. Bu tür üçgenlerin özelliklerini anlamak, problem çözme becerilerini geliştirir ve analitik düşünce yeteneğini artırır.
Sonuç
Dik üçgenler üzerine yaptığın bu derinlemesine inceleme, geometri konusundaki bilginin yanı sıra analitik düşünme yeteneğini de geliştirmiş. Bu tür konuları inceleyerek daha fazla bilgi edinmek her zaman faydalıdır. Geometriye olan ilginin artarak devam etmesi dileğiyle!
hipotenüsü 24 olan üçgeni incelerken, dik kenarların uzunluklarını bulmak için Pisagor Teoremi'nden faydalanmak oldukça faydalı. Dik kenarların karelerinin toplamı, hipotenüsün karesine eşit olduğundan, bu üçgenin özelliklerini anlamak ve çözümlemek için bu teoremi kullanmak şart.
Hüner,
Pisagor Teoremi'nin Önemi
Gerçekten de, hipotenüsü 24 olan bir dik üçgende dik kenarların uzunluklarını bulmak için Pisagor Teoremi'nden faydalanmak oldukça önemli. Teoremin temel prensibi, dik üçgenlerdeki kenar uzunlukları arasındaki ilişkiyi anlamamıza yardımcı oluyor.
Dik Kenarların Hesaplanması
Bu durumda, hipotenüsün karesi 576 eder (24² = 576). Dik kenarları a ve b olarak adlandıralım. Pisagor Teoremi'ne göre a² + b² = 576 eşitliğini kurabiliriz. Bu eşitlikten yola çıkarak, farklı değerler deneyerek a ve b'nin olası uzunluklarını bulabiliriz. Örneğin, a = 18 ve b = 12 değerleri bu durumu sağlayacaktır (18² + 12² = 576).
Sonuç
Pisagor Teoremi, üçgenin özelliklerini anlamak ve farklı senaryoları çözümlemek için güçlü bir araçtır. Bu teoremi kullanarak, hem matematiksel düşünme becerimizi geliştirebilir hem de geometri alanındaki kavrayışımızı artırabiliriz.
Bu tür problemleri çözmek, matematiksel düşünce yapısını ve analitik becerileri güçlendirmek için harika bir yoldur.
Dik üçgenin özelliklerini anladım fakat hipotenüsün dik kenarlara oranıyla ilgili bir örnek çözebilir misiniz? Özellikle 30-60-90 derecelik dik üçgende bu oranların nasıl işlediğini görmek istiyorum.
Merhaba Verâ,
Tabii ki, 30-60-90 derecelik dik üçgenin özelliklerini ve hipotenüsün dik kenarlara oranını açıklayalım. Bu tür üçgenlerde özel oranlar vardır:
1. 30 derece karşısındaki dik kenar, hipotenüsün yarısıdır.
2. 60 derece karşısındaki dik kenar, hipotenüsün √3/2 katıdır.
Örneğin, hipotenüsü 10 birim olan bir 30-60-90 üçgenini düşünelim:
- 30 derece karşısındaki dik kenar: 10 / 2 = 5 birim
- 60 derece karşısındaki dik kenar: 10 √3 / 2 ≈ 10 1.732 / 2 ≈ 8.66 birim
Bu oranlar her 30-60-90 üçgeni için geçerlidir. Umarım bu örnek, hipotenüs ve dik kenarlar arasındaki oranları anlamana yardımcı olur. İyi çalışmalar!