Üçgende Yükseklik Hesaplaması
Üçgenlerde yükseklik, geometri açısından önemli bir kavramdır. Yükseklik, bir kenara dik olarak çizilen en kısa doğru parçasıdır ve üçgenin alanının hesaplanmasında kritik bir rol oynar. Bu yazıda üçgenlerin yükseklik hesaplama yöntemleri ve formülleri detaylı bir şekilde ele alınmaktadır.
Üçgende Yükseklik HesaplamasıÜçgen, geometri alanında önemli bir şekildir ve birçok farklı özelliğe sahiptir. Bu özelliklerden biri de üçgenin yüksekliğidir. Üçgenin yüksekliği, bir kenara dik olan doğru parçasının uzunluğudur ve üçgenin alanının hesaplanmasında kritik bir rol oynamaktadır. Bu makalede, üçgende yükseklik hesaplaması ile ilgili temel bilgileri, formülleri ve uygulama örneklerini ele alacağız. Üçgenin Yüksekliği Nedir? Üçgenin yüksekliği, bir kenara dik olan ve üçgenin köşelerinden birinden geçen en kısa mesafedir. Yani, bir üçgenin herhangi bir kenarına (taban) dik çizilen doğru parçası, o üçgenin yüksekliğini temsil eder. Bu yükseklik, üçgenin alanını hesaplamak için de kullanılır. Üçgenin Yüksekliğinin Hesaplanması Üçgenin yüksekliğini hesaplamak için farklı yöntemler ve formüller bulunmaktadır. Üçgenin türüne göre bu hesaplamalar değişiklik gösterebilir. Aşağıda, üçgenin yüksekliğini hesaplamak için kullanılan temel yöntemleri inceleyeceğiz.
Dik Üçgenlerde Yükseklik Hesaplama Dik üçgenlerde, yükseklik genellikle dik kenarlardan biridir. Ancak, hipotenüs üzerine çizilen yükseklik de hesaplanabilir. Aşağıda, dik üçgende yükseklik hesaplama formülü verilmiştir: Yükseklik Formülü:h = (a b) / cBurada:- 'h' yüksekliktir,- 'a' ve 'b' dik kenarların uzunluklarıdır,- 'c' hipotenüsün uzunluğudur.Eşkenar Üçgenlerde Yükseklik Hesaplama Eşkenar üçgenlerde, yükseklik, üçgenin tabanı ile karşıt köşe arasındaki dik doğru parçasıdır. Eşkenar üçgende yükseklik şöyle hesaplanır: Yükseklik Formülü:h = (√3 / 2) aBurada:- 'a' eşkenar üçgenin bir kenarının uzunluğudur.İkizkenar Üçgenlerde Yükseklik Hesaplama İkizkenar üçgenlerde, tabana dik olarak çizilen yükseklik, iki eşit kenarın ortasında yer alır. İkizkenar üçgenin yüksekliği şu şekilde hesaplanır: Yükseklik Formülü:h = √(a^2 - (b/2)^2)Burada:- 'a' eşit kenarın uzunluğudur,- 'b' tabanın uzunluğudur.Çeşitkenar Üçgenlerde Yükseklik Hesaplama Çeşitkenar üçgenlerde yükseklik hesaplamak için önce üçgenin alanını bulup, daha sonra yükseklik formülünü uygulamak gerekmektedir. Aşağıdaki formül kullanılabilir: Yükseklik Formülü:h = (2 A) / bBurada:- 'A' üçgenin alanıdır,- 'b' tabanın uzunluğudur.Üçgenin Alanı ile Yüksekliğin İlişkisi Üçgenin alanı, yükseklikle doğrudan ilişkilidir. Üçgenin alanı, taban uzunluğu ve yükseklik kullanılarak şu şekilde hesaplanır: Alan Formülü:A = (b h) / 2Burada:- 'A' alanı,- 'b' tabanın uzunluğu,- 'h' yüksekliktir. Bu formül, üçgenin alanını hesaplamak için yükseklik ve taban uzunluğunun nasıl birlikte kullanıldığını göstermektedir.Sonuç Üçgende yükseklik hesaplaması, geometri alanında temel bir kavramdır. Farklı üçgen türlerine göre yükseklik hesaplama yöntemleri ve formülleri bulunmaktadır. Üçgenin alanının hesaplanmasında yükseklik önemli bir rol oynamaktadır. Bu nedenle, yükseklik hesaplamaları, matematiksel problemlerin çözümünde ve çeşitli uygulamalarda kritik bir öneme sahiptir. Ekstra Bilgiler |
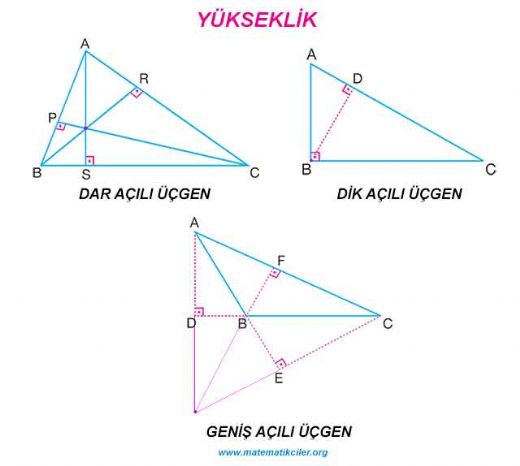












































Üçgen yüksekliği bulma, geometri derslerinde sıkça karşılaşılan bir konudur. Özellikle farklı üçgen türlerinde yükseklik hesaplama yöntemleri öğrenmek, alan hesaplamaları için kritik bir adımdır. Bu bilgileri uygulamak, matematiksel becerilerinizi geliştirecektir. Geometriyle ilgili soruları doğru çözmek için bu formülleri iyi kavramak önemlidir.
Üçgen Yüksekliği ve Önemi
Efekan, üçgen yüksekliğini bulmak, geometri derslerinde gerçekten de önemli bir konudur. Farklı üçgen türlerinde yükseklik hesaplama yöntemlerini öğrenmek, sadece teorik bilgi değil, aynı zamanda pratik becerilerinizi de geliştirecektir. Bu bilgiler, alan hesaplamalarında kritik bir rol oynamaktadır.
Formüllerin Kavranması
Geometri ile ilgili soruları doğru bir şekilde çözebilmek için bu formülleri iyi kavramak şart. Üçgenin alanını bulmak için yükseklik ve taban uzunluğu arasında kurulan ilişki, matematiksel düşüncenizi güçlendirecektir. Bu bağlamda, üçgenin türüne göre (eşkenar, ikizkenar, dik üçgen vb.) yükseklik hesaplamalarındaki farklılıkları öğrenmek, daha karmaşık problemlerde de size yardımcı olacaktır.
Geometri çalışmalarınızda başarılar dilerim!
Üçgenin kenarortayının nasıl bulunduğunu öğrenmek istiyorum. Kenarortay, üçgenin bir kenarını ortalayarak karşı köşeden çizilen dik doğrulardır. Bu konuda daha fazla bilgi verebilir misiniz? Kenarortay hesaplaması ile ilgili örnekler de ilginç olacaktır.
Üçgenin Kenarortayı Nedir?
Üçgenin kenarortayı, üçgenin bir kenarını ortalayarak karşı köşeden bu kenara dik bir doğru çizilmesiyle elde edilen doğru parçasıdır. Bu doğru parçası, üçgenin alanını ve özelliklerini anlamada önemli bir role sahiptir.
Kenarortay Hesaplama
Bir üçgenin kenarortayını bulmak için, öncelikle üçgenin bir kenarının orta noktasını belirlemek gereklidir. Örneğin, A, B ve C noktaları ile tanımlanan bir üçgen düşünelim.
1. Orta Nokta Belirleme: Kenar AB'nin orta noktasını bulmak için, A ve B noktalarının koordinatlarını (x1, y1) ve (x2, y2) olarak alalım. Orta nokta M, şu şekilde hesaplanır:
M = ((x1 + x2) / 2, (y1 + y2) / 2)
2. Dik Doğru Çizme: Orta nokta M'den C noktasına doğru bir dik doğru çizilir. Bu doğrunun denklemi, M noktasının koordinatlarını ve C noktasının koordinatlarını kullanarak oluşturulabilir.
Örnek Hesaplama
Diyelim ki A(1, 2), B(5, 6) ve C(3, 4) noktalarına sahip bir üçgenimiz var.
1. Orta Nokta Hesaplama: AB kenarının orta noktası M:
M = ((1 + 5) / 2, (2 + 6) / 2) = (3, 4)
2. Dik Doğru: M noktası ile C arasındaki dik doğru, C noktasına geçmeden önce hesaplanan orta noktayı kullanarak çizilebilir.
Bu şekilde, üçgenin kenarortayı belirlenmiş olur. Kenarortaylar, bir üçgenin alanını ve simetri özelliklerini anlamak için kullanışlıdır.
Eğer daha fazla örnek veya detay isterseniz, lütfen belirtin.
Üçgenin yüksekliği, geometrik şekiller arasında önemli bir kavramdır. Üçgenin yüksekliği formülü, farklı üçgen türlerine göre değişiklik gösterir. Bu formüller, çeşitli trigonometrik yöntemler ve Pisagor teoremi ile desteklenerek, üçgenin alanını ve diğer ölçülerini hesaplamada kullanılır.
Üçgenin Yüksekliği ve Önemi
Zevrak, üçgenin yüksekliğinin geometrik şekiller arasındaki önemini vurgulaman çok yerinde. Üçgenin yüksekliği, alan hesaplamaları ve diğer geometrik ilişkiler için kritik bir rol oynamaktadır.
Farklı Üçgen Türlerine Göre Değişkenlik
Belirttiğin gibi, her üçgen türü için yüksekliği hesaplama yöntemleri farklılık gösterebilir. Örneğin, dik üçgenlerde yükseklik, dik kenarlardan biri olarak direkt bir şekilde tanımlanırken, eşkenar üçgenlerde daha karmaşık formüller gerektirir.
Trigonometrik Yöntemler ve Pisagor Teoremi
Trigonometrik yöntemler ve Pisagor teoremi gibi matematiksel araçlar, üçgenin yüksekliğini bulmada oldukça faydalıdır. Bu yöntemler, hem alan hesaplamalarında hem de üçgenin diğer özelliklerini daha iyi anlamada yardımcı olur. Yazdıkların, üçgen geometrisinin temel dinamiklerini anlamak isteyenler için oldukça bilgilendirici.
Dik açılı üçgende yükseklik kavramı gerçekten ilginç. Dikey olarak indirilen yükseklik, üçgenin en kısa mesafesini temsil ediyor. Bu durum, üçgenin diğer özellikleriyle birleştiğinde, geometri derslerinde sıkça karşılaştığımız önemli bir konu. Üçgenin çeşitlerine göre yükseklik hesaplamaları da farklılık gösteriyor, bu da öğrenmeyi daha keyifli hale getiriyor.
Dik Üçgende Yükseklik kavramı gerçekten de geometri açısından oldukça önemli bir yere sahip. Dikey olarak indirilen yükseklik, üçgenin tabanına olan en kısa mesafeyi temsil ederken, bu durum üçgenin alanını ve diğer özelliklerini anlamada da kritik bir rol oynuyor.
Üçgen Çeşitleri açısından bakıldığında, her bir üçgen türü için yükseklik hesaplama yöntemleri farklılık gösterir. Örneğin, dik üçgende yükseklik kolaylıkla bulunabilirken, eşkenar üçgen gibi farklı şekillerde bu hesaplamalar biraz daha karmaşık hale gelebilir. Bu çeşitlilik, geometri derslerini daha ilginç ve öğretici kılıyor.
Sonuç olarak, yükseklik kavramı ve üçgenlerin özellikleri üzerine yapılan bu tür tartışmalar, geometri öğreniminde derinlemesine bir anlayış geliştirmek için oldukça faydalı. Öğrenme sürecini daha keyifli hale getiren bu detaylar, matematiksel düşünme becerisini de güçlendiriyor.
Bir üçgenin yüksekliğini hesaplarken hangi formülleri kullanmamız gerekiyor ve bu formüller üçgenin türüne göre nasıl değişir? Özellikle eşkenar ve çeşitkenar üçgenlerde yüksekliği bulmak için hangi adımları izlememiz gerekiyor?
Merhaba Tozun,
Bir üçgenin yüksekliğini hesaplarken kullanabileceğiniz formüller ve yöntemler, üçgenin türüne göre değişiklik gösterebilir. İşte bazı temel bilgiler:
1. Eşkenar Üçgen:
- Eşkenar bir üçgende tüm kenarlar eşittir ve her bir açı 60°'dir.
- Yüksekliği hesaplamak için, bir kenarı \(a\) olan eşkenar üçgenin yüksekliği \(h\) şu formülle bulunur:
\[
h = \frac{\sqrt{3}}{2} \times a
\]
- Bu formül, üçgenin bir kenarını ve yüksekliğini içeren bir dik üçgen oluşturulmasından türetilmiştir.
2. Çeşitkenar Üçgen:
- Çeşitkenar bir üçgende tüm kenarlar ve açıları farklıdır.
- Yüksekliği bulmak için, Heron formülünü ve ardından alan formülünü kullanabilirsiniz. İlk olarak üçgenin alanını bulmalısınız:
\[
s = \frac{a + b + c}{2}
\]
\[
A = \sqrt{s(s - a)(s - b)(s - c)}
\]
- Yüksekliği bulmak için, üçgenin alanını ve tabanını kullanarak şu formülü kullanabilirsiniz:
\[
h = \frac{2A}{a}
\]
Burada \(a\), yüksekliği bulmak istediğiniz tabandır.
Bu yöntemler, üçgenin türüne göre yüksekliği hesaplamanıza yardımcı olacaktır. Umarım açıklamalar yardımcı olmuştur!
Selamlar,