
Üçgende Kenarortay Formülleri
Üçgen geometrisi, kenarortaylar sayesinde önemli hesaplamalar ve analizler yapılmasını sağlar. Kenarortaylar, üçgenin köşelerinden karşı kenar ortalarına çizilen doğrular olup, alan hesaplamaları ve mühendislik uygulamalarında kritik bir rol oynar. Bu yazıda kenarortayların özellikleri ve formülleri ele alınmaktadır.
Üçgende Kenarortay FormülleriÜçgen geometrisi, matematiksel ve fiziksel uygulamalar açısından önemli bir yere sahiptir. Üçgenin kenarortayları, üçgenin köşelerinden karşı kenar ortalarına çizilen doğru parçalarıdır. Bu yazıda, üçgende kenarortay formülleri, özellikleri ve uygulamaları detaylı bir şekilde incelenecektir. Kenarortay Nedir? Kenarortay, bir üçgenin bir köşesinden karşı kenarın ortasına çizilen doğru parçasıdır. Her üçgenin üç adet kenarortayı bulunmaktadır. Kenarortaylar, üçgenin alanını ve çeşitli geometrik özelliklerini hesaplamak için kullanılır. Kenarortayların Özellikleri Kenarortayların bazı önemli özellikleri şunlardır:
Kenarortay Formülleri Kenarortay uzunlukları, üçgenin kenar uzunlukları kullanılarak hesaplanabilir. Bir üçgenin kenarortay uzunluğunu hesaplamak için aşağıdaki formül kullanılabilir: Kenarortay (m) = √(2a² + 2b² - c²) / 4 Burada "a" ve "b" kenar uzunlukları, "c" ise karşı kenarın uzunluğudur. Bu formül, kenarortayların uzunluğunu hesaplamak için basit bir yöntem sunar. Kenarortayların Uygulamaları Kenarortaylar, birçok alanda uygulanabilir:
Sonuç Üçgende kenarortaylar, temel geometrik kavramlar arasında yer almakta ve birçok uygulama alanında önemli bir rol oynamaktadır. Kenarortay formülleri, üçgenin özelliklerini anlamak ve çeşitli hesaplamalar gerçekleştirmek için kritik öneme sahiptir. Geometri alanında yapılan çalışmalar ve araştırmalar, kenarortayların özelliklerini daha iyi anlamamıza ve uygulamalarını genişletmemize yardımcı olmaktadır. Ek bilgiler: Üçgenin kenarortayları ile ilgili daha fazla bilgi edinmek için, geometri kitapları ve kaynakları incelenebilir. Ayrıca, çeşitli matematiksel yazılımlar ile üçgenin özellikleri daha detaylı bir şekilde analiz edilebilir. |
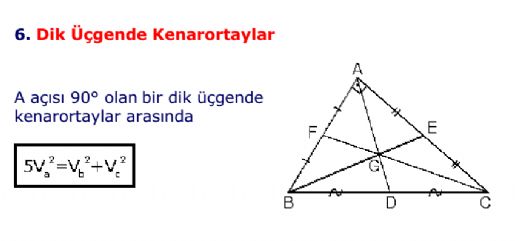















































Üçgende kenarortayların özellikleri gerçekten ilginç. Kenarortayların, üçgenin alanını eşit parçalara böldüğünü duymak, bu geometrik şekillerin ne kadar düzenli olduğunu gösteriyor. Özellikle ağırlık merkezinin üçgeni 2:1 oranında böldüğünü öğrenmek, üçgenin simetrisinin ve dengesinin ne kadar önemli olduğunu bir kez daha hatırlatıyor. Dik üçgende, hipotenüse çizilen kenarortayın uzunluğunun, hipotenüsün yarısına eşit olması ise oldukça dikkat çekici bir özellik. Bu tür özelliklerin, matematiksel problemlerde nasıl kullanıldığını merak ediyorum. Kenarortayların birbirleriyle kesişimlerinin oluşturduğu ilişkiler de oldukça ilginç görünüyor; bu tür ilişkileri nasıl uygulayabileceğimize dair örnekler verebilir misin?
Kenarortayların Özellikleri
Merhaba Aramcan, kenarortayların özellikleri gerçekten de matematikte ve geometri derslerinde önemli bir yere sahip. Üçgende kenarortayların oluşturduğu alan bölünmesi, üçgenin simetri ve dengesine dair harika bilgiler sunuyor. Ayrıca, ağırlık merkezinin üçgeni 2:1 oranında bölmesi, bu dengenin ne kadar etkili olduğunu gösteriyor.
Dik Üçgende Kenarortay
Dik üçgende hipotenüse çizilen kenarortay uzunluğunun hipotenüsün yarısına eşit olması, öğrencilere ve matematik meraklılarına çeşitli problemleri çözme konusunda yardımcı olabiliyor. Bu özellik, dik üçgenler üzerindeki hesaplamalarda pratik bir kolaylık sağlıyor.
Matematiksel Problemlerde Kullanım
Bu tür özelliklerin matematiksel problemlerde nasıl kullanılabileceği ile ilgili birkaç örnek vermek gerekirse; kenarortayların özelliklerini kullanarak alan hesaplamaları yapabiliriz. Ayrıca, kenarortayların kesişim noktaları olan ağırlık merkezi ile ilgili problemler çözmek, öğrencilerin bu kavramları daha iyi anlamalarına yardımcı olabilir. Örneğin, bir üçgende kenarortayları kullanarak alan oranlarını bulmak veya ağırlık merkezinin koordinatlarını belirlemek gibi uygulamalar oldukça faydalı olabilir.
Bu özelliklerin daha ileri düzeydeki geometri ve analitik geometri konularında da nasıl işlediğini incelemek, geometrik şekillerle ilgili bilgi birikimini artıracaktır. Geometri dersi sırasında bu tür konuları derinlemesine öğrenmek, matematiksel düşünmeyi geliştirebilir.