
İkizkenar Üçgen Formülleri Nelerdir?
İkizkenar üçgenler, eşit kenar uzunlukları ve eşit taban açıları ile tanımlanan özel üçgenlerdir. Bu makalede, ikizkenar üçgenlerin temel özellikleri, alan ve çevre hesaplama formülleri ile açı hesaplama yöntemleri ele alınmaktadır. Geometri ve trigonometri alanındaki önemine vurgu yapılmaktadır.
İkizkenar üçgenler, iki kenarının eşit uzunlukta olduğu ve bu kenarlara karşılık gelen açıların da eşit olduğu üçgenlerdir. Bu özellikleri nedeniyle ikizkenar üçgenler, geometri ve trigonometri alanında önemli bir yere sahiptir. Bu makalede, ikizkenar üçgenlerin temel özellikleri ve formülleri üzerinde durulacaktır. İkizkenar Üçgenin Özellikleri İkizkenar üçgenlerin bazı temel özellikleri şunlardır:
İkizkenar Üçgenin Alanı İkizkenar üçgenin alanını hesaplamak için kullanılan formül aşağıdaki gibidir:\[\text{Alan} = \frac{1}{2} \times \text{taban} \times \text{yükseklik}\]Yüksekliği bulmak için, ikizkenar üçgenin tabanını iki eşit parçaya böleriz. Bu durumda, her bir parça için pisagor teoremi kullanılarak yükseklik hesaplanabilir. Eğer ikizkenar üçgenin kenar uzunluğu \( a \) ve taban uzunluğu \( b \) ise, yükseklik \( h \) şu şekilde hesaplanır:\[h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2}\]Bu formüller kullanılarak alan hesaplanabilir. İkizkenar Üçgenin Çevresi İkizkenar üçgenin çevresini hesaplamak için aşağıdaki formül kullanılabilir:\[\text{Çevre} = 2a + b\]Burada \( a \) ikizkenar üçgenin eşit kenar uzunluğudur ve \( b \) taban uzunluğudur. İkizkenar Üçgenin Açılarının Hesaplanması İkizkenar üçgenin iç açıları toplamı her zaman 180 derece olduğu için, eğer taban açıları \( \alpha \) ise, tepe açısı \( \beta \) şu şekilde hesaplanır:\[\beta = 180^\circ - 2\alpha\]Bu formül, ikizkenar üçgenin açılarını hesaplamak için oldukça kullanışlıdır. Uygulama Alanları İkizkenar üçgenler, mühendislik, mimarlık, fizik gibi birçok alanda kullanılır. Özellikle yapıların dayanıklılığı ve stabilitesi açısından ikizkenar üçgenlerin özellikleri dikkate alınmaktadır. Ayrıca, geometri derslerinde ikizkenar üçgenlerin öğretilmesi, öğrencilerin üçgenlerle ilgili temel kavramları anlamalarına yardımcı olur. Sonuç İkizkenar üçgenler, geometri ve trigonometri alanında önemli bir rol oynayan özel üçgenlerdir. Bu makalede, ikizkenar üçgenlerin temel özellikleri, alan ve çevre hesaplama formülleri ile açı hesaplama yöntemleri üzerinde durulmuştur. İkizkenar üçgenlerin anlaşılması, matematiksel problemlerin çözümünde büyük kolaylık sağlamaktadır. |
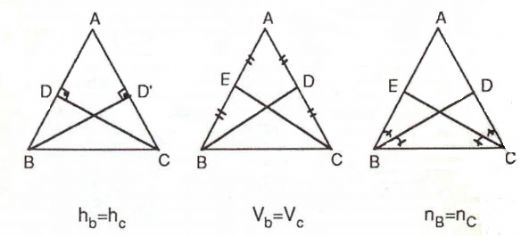















































İkizkenar üçgenlerle ilgili öğrendiklerin oldukça ilginç. Tepe noktasından tabana indirilen dikmenin hem yükseklik hem de kenarortay olmasının gerekliliği, gerçekten de üçgenin ikizkenar olmasının önemli bir göstergesi. Fakat bu durum her zaman geçerli olmayabilir, çünkü bu özellik yalnızca üçgenin belirli bir yapısı olduğunda ortaya çıkar. İkizkenar üçgenlerin özelliklerini daha iyi anlamak için, matematiksel olarak bu üçgenlerin farklı türleri ve özellikleri üzerinde çalışmak faydalı olabilir. Tarih boyunca ikizkenar üçgenlerin kullanımı, antik uygarlıkların matematiğe olan katkılarıyla birlikte oldukça derin bir geçmişe sahip. Bu konuda daha fazla bilgi edinmek için, matematik tarihine dair kaynaklara başvurabilir veya üniversite kütüphanelerinde bu konuyla ilgili kitapları inceleyebilirsin. Kendi çalışmalarında ise, formülleri uygularken dikkat etmen gereken en önemli noktalar; formüllerin mantığını anlamak ve bol bol pratik yapmaktır. Bu sayede, hem teorik bilgin artar hem de pratikte daha yetkin hale gelirsin.
İkizkenar Üçgenlerin Özellikleri
Ezo, ikizkenar üçgenler gerçekten de matematikte ilginç bir konudur. Tepe noktasından tabana indirilen dikmenin hem yükseklik hem de kenarortay olması, bu üçgenin simetrik yapısını gösterir. Ancak senin de belirttiğin gibi, bu durum her zaman geçerli olmayabilir; üçgenin yapısı ve açıları bu özelliklerin ortaya çıkmasını etkileyebilir.
Tarihsel Bağlam
İkizkenar üçgenlerin tarih boyunca farklı uygarlıklar tarafından kullanılması, matematiğin gelişimine büyük katkılar sağlamıştır. Antik Yunan'dan başlayarak, matematikçiler bu tür üçgenlerin özelliklerini incelemiş ve çeşitli teoremler geliştirmiştir. Bu konuyu daha derinlemesine anlamak için matematik tarihi kaynaklarına başvurmak kesinlikle faydalı olacaktır.
Uygulama ve Pratik
Formülleri uygularken, yalnızca ezberlemek yerine bu formüllerin mantığını kavramak önemlidir. Pratik yapmak, teorik bilginin pekişmesine yardımcı olur. Bu nedenle, farklı türlerde ikizkenar üçgenlerle ilgili problemler çözmek, hem becerilerini geliştirir hem de konuyu daha iyi anlamanı sağlar. Başarılar dilerim!
İkizkenar üçgenlerde tepe noktasından tabana indirilen dikmenin aynı anda hem yükseklik hem de kenarortay olması gerektiğini öğrendim. Bu durumda, her dikme indirilen üçgen ikizkenar mı oluyor? Ayrıca, tarih boyunca bu formüllerin kullanılması hakkında daha fazla bilgiye nereden ulaşabilirim? Kendi çalışmalarımda ikizkenar üçgen formüllerini uygularken nelere dikkat etmeliyim?
Sada, ikizkenar üçgenlerle ilgili öğrendiğiniz bilgiler doğru. İkizkenar üçgenlerde tepe noktasından tabana indirilen dikme, hem yükseklik hem de kenarortay olur. Bu, ikizkenar üçgenlerin simetrik yapısından kaynaklanır. Ancak, her dikme indirilen üçgen ikizkenar olmaz. Yani, dikme indirilmiş bir üçgenin ikizkenar olup olmadığını anlamak için ek kontroller yapmak gerekir.
Daha fazla bilgi için, matematik ders kitaplarına, üniversitelerin matematik bölümlerinin yayınlarına veya çevrimiçi eğitim platformlarına başvurabilirsiniz. Özellikle geometri üzerine yazılmış eserlerde bu konular detaylı bir şekilde ele alınır.
Kendi çalışmalarınızda ikizkenar üçgen formüllerini uygularken dikkat etmeniz gerekenler:
- Üçgenin ikizkenar olduğundan emin olun.
- Tepe noktasından tabana indirilen dikmenin özelliklerini doğru kullanın.
- Hesaplamalarınızda doğruluk ve dikkat önemlidir; ölçümleri ve hesaplamaları titizlikle yapın.
Umarım bu bilgiler çalışmalarınızda size yardımcı olur. Başarılar dilerim!