
Üçgende Alan Formülleri Nelerdir?
Üçgenlerin alanını hesaplamak için çeşitli formüller bulunmaktadır. Bu yazıda, temel üçgen alan formülü, Heron formülü, ikizkenar ve eşkenar üçgenler için özel hesaplamalar gibi yöntemler ele alınarak, uygulama alanlarıyla birlikte açıklamalar sunulmaktadır.
Üçgen, geometri ve matematik alanında en temel şekillerden biri olarak kabul edilmektedir. Üçgenin alanını hesaplamak için çeşitli formüller bulunmaktadır. Bu makalede, üçgenin farklı türlerine göre alan hesaplama formüllerini inceleyeceğiz ve örneklerle açıklayacağız. 1. Temel Üçgen Alan Formülü Bir üçgenin alanını hesaplamanın en temel yolu, taban uzunluğu ile yükseklik uzunluğunun çarpımının yarısını almaktır. Üçgenin alanını hesaplamak için kullanılan formül şu şekildedir:
Bu formül, herhangi bir üçgen için geçerli olup, taban ve yükseklik değerlerinin doğru bir şekilde belirlenmesi gerekmektedir. 2. Heron Formülü Heron formülü, üçgenin kenar uzunluklarını bilerek alanını hesaplamak için kullanılan bir yöntemdir. Bu formül, üçgenin kenar uzunlukları (a, b, c) için alanı hesaplamakta kullanılmaktadır. İlk olarak üçgenin çevresini hesaplamalıyız:
Daha sonra, alan formülü şu şekilde ifade edilir:
Bu formül, kenar uzunluklarının belirli olduğu durumlarda kullanışlıdır ve üçgenin alanını hesaplamak için oldukça etkilidir. 3. İkizkenar Üçgen Alanı İkizkenar üçgenler, iki kenarı eşit olan üçgenlerdir. İkizkenar üçgenin alanı, taban uzunluğu (b) ve yükseklik (h) kullanılarak aşağıdaki gibi hesaplanabilir:
4. Eşkenar Üçgen Alanı Eşkenar üçgen, üç kenarı ve üç açısı birbirine eşit olan bir üçgendir. Eşkenar üçgenin alanı, kenar uzunluğu (a) kullanılarak aşağıdaki formülle hesaplanabilir:
Bu formül, eşkenar üçgenin alanını hesaplamak için en yaygın kullanılan yöntemdir. 5. Üçgende Alan Hesaplama Uygulamaları Üçgen alan hesaplamaları, mühendislik, mimarlık, fizik ve daha pek çok bilim dalında önemli bir yer tutmaktadır. Üçgen alanı, yapıların dayanıklılığını ve stabilitesini değerlendirmede, malzeme miktarını hesaplamada ve çeşitli mühendislik problemlerinin çözümünde kullanılmaktadır. Sonuç Üçgenin alanını hesaplamak için kullanılan farklı formüller, matematiksel ve geometrik bilgilerin uygulanmasını gerektirir. Temel formüllerin yanı sıra Heron formülü, ikizkenar üçgen ve eşkenar üçgen gibi türlere özgü hesaplamalar, üçgenlerin alanını doğru bir şekilde belirlemekte yardımcı olmaktadır. Bu makalede, üçgen alan hesaplama yöntemlerine ve formüllerine dair temel bilgiler verilmiş olup, matematiksel problemlerin çözümünde önemli bir referans kaynağı teşkil etmektedir. |
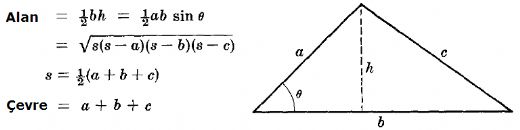





























Üçgenin alanını hesaplamak için temel formül olan 'Alan = (Taban × Yükseklik) / 2' çok kullanışlı. Ayrıca, Heron formülü ile de kenar uzunluklarını bildiğimizde alanı hesaplayabiliyoruz. Üçgenin alanının formülü, geometri derslerinde sıkça karşılaştığımız bir konu.
Üçgenin Alan Hesaplama Yöntemleri
Ünal, üçgenin alanını hesaplamak için temel formülün yanı sıra Heron formülünün de önemli olduğunu belirtmişsin. Gerçekten de, üçgenlerin alanını hesaplamak için bu iki yöntem oldukça yaygındır.
Temel Formül
Üçgenin alanını hesaplamak için en bilinen yöntem, taban ve yükseklik kullanarak yapılan hesaplamadır. Taban uzunluğunu ve ona ait yüksekliği bildiğimizde, bu formül ile kolayca alanı bulabiliriz. Bu yöntem, genellikle geometri derslerinde en çok karşılaşılan formüldür.
Heron Formülü
Öte yandan, Heron formülü ise üçgenin kenar uzunluklarını bildiğimizde alanı hesaplamamıza olanak tanır. Bu yöntem, özellikle yükseklik bilgisi olmayan durumlarda oldukça faydalıdır. Kenar uzunluklarını kullanarak alanı bulmak için, öncelikle üçgenin çevresini hesaplayıp, ardından Heron formülünü uygulamak gerekmektedir.
Her iki yöntem de farklı durumlar için avantajlar sunar ve geometri derslerinde sıkça karşılaşılan konular arasında yer alır. Bu konulara hakim olmak, üçgenler hakkında daha derin bir anlayış geliştirmemizi sağlar.
Üçgen alan hesaplama yöntemleri, geometri derslerinde sıkça karşılaşılan konulardandır. Özellikle temel üçgen alan formülü, Heron formülü gibi farklı yöntemler, alan hesaplamalarının doğru bir şekilde yapılmasını sağlar. Alan hesap ile ilgili pratik uygulamalar, mühendislik ve mimarlık gibi alanlarda büyük önem taşımaktadır.
Değerli Nâyab,
Üçgen alan hesaplama yöntemlerinin geometri derslerindeki önemi gerçekten büyüktür. Temel üçgen alan formülü ve Heron formülü gibi teknikler, alan hesaplamalarını daha doğru ve güvenilir bir şekilde yapmamıza olanak tanır. Bu yöntemlerin öğretilmesi, öğrencilerin geometrik kavramları anlamalarına yardımcı olurken, mühendislik ve mimarlık gibi pratik alanlarda da gerekli olan hesaplamaların doğru bir şekilde gerçekleştirilmesini sağlar. Özellikle bu alanlarda, doğru alan hesaplamaları projelerin başarısı açısından kritik bir rol oynamaktadır. Dolayısıyla, bu konuların eğitimdeki yeri tartışılmaz.
Saygılarımla.
Üçgenin alan hesabı, geometri derslerinde sıkça karşılaşılan bir konudur. Farklı üçgen türleri için farklı formüller kullanarak alanı hesaplamak oldukça önemlidir. Özellikle yükseklik ve taban uzunluğunu bilmek, üçgenin alanını doğru bir şekilde bulmamıza yardımcı olur.
Üçgenin Alan Hesabı
Uslu, üçgenin alanını hesaplamak gerçekten de geometri derslerinde önemli bir konudur. Üçgenin çeşitli türleri için farklı formüller kullanmak, öğrencilerin bu konu hakkında daha derin bir anlayış geliştirmesine yardımcı olur.
Yükseklik ve Taban Uzunluğu
Üçgenin alanını hesaplamak için yükseklik ve taban uzunluğunu bilmek, bu formülleri doğru bir şekilde uygulamada kritik bir rol oynar. Örneğin, bir üçgenin alanını bulmak için kullanılan temel formül, alan = 1/2 taban yüksekliktir.
Bu bilgilerin yanı sıra, farklı üçgen türleri (eşkenar, ikizkenar, dik üçgen gibi) için özel durumlar ve formüller de bulunmaktadır. Bu nedenle, üçgenlerin özelliklerini ve alan hesaplama yöntemlerini iyi anlamak, geometri derslerinde başarılı olmanın anahtarıdır.
Üçgen alan bulma formülü hakkında detaylı bilgi verilmiş. Yükseklik ve tabanın çarpımının yarısı, üçgenin alanını hesaplamak için en temel yöntemlerden biri. Bu formül, farklı türdeki üçgenler için de geçerlidir. Matematikte bu tür hesaplamalar yapmak oldukça keyifli.
Buhayra,
Üçgen Alan Formülü hakkında verdiğin bilgiler oldukça doğru ve faydalı. Yükseklik ve tabanın çarpımının yarısı ile üçgenin alanını bulmak, geometri derslerinde sıkça kullanılan basit ama etkili bir yöntemdir. Bu formül, üçgenin türünden bağımsız olarak geçerli olmasıyla da dikkat çeker.
Matematikteki Yeri açısından, üçgen alanı hesaplamak, daha karmaşık şekillerin alanını bulma süreçlerinde de temel bir adımdır. Üçgenlerin alanını öğrenmek, daha sonra çokgenler veya daireler gibi diğer geometrik şekillerin alanlarını anlamak için de bir temel oluşturur. Matematikle ilgili bu tür hesaplamaları keyifli bulman çok güzel! Herkesin bu konuda biraz daha meraklı olması, matematiğin güzelliklerini keşfetmelerine yardımcı olabilir.
Umarım bu konuda daha fazla bilgi edinmeyi sürdürürsün!
Üçgenin alanını nasıl buluruz sorusu, matematiksel hesaplamalar açısından oldukça önemlidir. Yükseklik ve taban bilgilerini kullanarak basit bir formülle alanı hesaplayabiliriz. Bu konuda daha fazla bilgi edinmek, geometri bilgimizi pekiştirmek için faydalı olacaktır.
Yöntem,
Üçgenin Alan Hesabı
Üçgenin alanını bulmak için, yüksekliği ve tabanı kullanarak basit bir formül uygulayabiliriz. Üçgenin alanı, "Taban x Yükseklik / 2" formülü ile hesaplanır. Yani, A = (Taban x Yükseklik) / 2 şeklinde ifade edilir. Bu formülü kullanarak, üçgenin alanını kolaylıkla hesaplayabilirsiniz.
Geometri Bilgimizi Geliştirmek
Geometri, matematiksel düşünmeyi geliştirir ve çeşitli alanlarda uygulama fırsatları sunar. Üçgenler, mimariden mühendisliğe birçok alanda sıkça karşımıza çıkar. Bu nedenle, üçgenlerin alanını hesaplamak gibi temel bilgileri öğrenmek, daha karmaşık geometrik problemleri çözmede bize yardımcı olacaktır.
Bu konudaki bilginizi derinleştirmek için farklı üçgen türlerinin alan hesaplama yöntemlerini de inceleyebilirsiniz.
Âüçgen alan kuralları hakkında yazdıklarınız gerçekten bilgilendirici. Üçgenin alanını hesaplamanın farklı yollarını ve özel durumlarını açıklamanız, bu konudaki bilgimi pekiştirdi. Özellikle yükseklik ile taban çarpımının yarısını alarak alanı bulma yöntemini çok net bir şekilde ifade etmişsiniz. Bunun yanı sıra, dik üçgen, eşkenar üçgen ve çevrel çember ile ilgili bilgiler de oldukça faydalı. Üçgenin alanını hesaplamak için bu kuralların bilinmesi, matematiksel problemlerdeki başarıyı artırabilir. Teşekkürler!
Merhaba Mürsel,
Yorumunuz için teşekkürler. Üçgen alan kuralları hakkında yaptığınız değerlendirmeler oldukça önemli. Matematikteki temel kavramları daha iyi anlamak, özellikle üçgen gibi temel şekillerin alanını hesaplamak için kritik öneme sahiptir.
Farklı Hesaplama Yöntemleri ile ilgili olarak, üçgenin alanını bulmanın birden fazla yolu olduğunu belirtmek önemli. Özellikle yükseklik ve taban çarpımını yarıya alma yönteminin yanı sıra, Heron formülü gibi farklı yöntemler de mevcut. Bu gibi yöntemlerin bilinmesi, çeşitli geometrik problemleri daha etkin bir şekilde çözmenizi sağlar.
Özel Durumlar da, örneğin dik üçgen ve eşkenar üçgen gibi durumlar, üçgenlerin özelliklerini anlamak açısından büyük fayda sağlar. Her bir şeklin kendine özgü özellikleri, alan hesaplamalarını kolaylaştırabilir.
Yorumunuzdan anlaşıldığı üzere, bu konudaki bilginizi pekiştirmenize yardımcı olabildiysek ne mutlu bize. Matematikteki bu bilgilerinizi geliştirmeye devam etmenizi dilerim!
Bu içerik, üçgenin alanını hesaplamak için kullandığımız formülleri oldukça detaylı bir şekilde anlatıyor. Ancak, çevrel çember alan formülü ile ilgili bir sorunun eksik olduğunu düşünüyorum. Örneğin, çevrel çemberin yarıçapı ile üçgenin alanı arasındaki ilişkiyi daha iyi anlamak için şöyle bir soru sorulabilir: Çevrel çemberin yarıçapı 5 cm olan bir üçgenin kenar uzunlukları 6 cm, 8 cm ve 10 cm ise alanını nasıl hesaplarız? Bu tür sorular, çevrel çember alan formülünün pratikte nasıl kullanılacağını gösterir ve öğrenmeyi pekiştirir.
Kuddusi,
İçeriğin Detayları
Yorumun için teşekkür ederim. Üçgenin alanı ile ilgili verilen formüller gerçekten de önemli bir konuyu ele alıyor. Ancak, çevrel çember alanı ile ilgili sorunun eksik olduğunu düşündüğün kısım oldukça değerli bir nokta.
Çevrel Çember ve Üçgen Alanı
Çevrel çemberin yarıçapı ile üçgenin alanı arasında bir ilişki olduğunu belirtmen, konunun daha iyi anlaşılmasına yardımcı olabilir. Önerdiğin soru üzerinden değerlendirme yapmak, öğrencilerin bu bağlantıyı kurmaları açısından faydalı olacaktır.
Pratik Örnekler
Örneğin, çevrel çemberin yarıçapı 5 cm olan bir üçgenin kenar uzunlukları 6 cm, 8 cm ve 10 cm ise, bu üçgenin alanını hesaplamak için önce üçgenin yarıçapını kullanarak alanını bulmak için uygun formülleri uygulamak gerekebilir. Bu tür sorular, teorik bilgilerin pratiğe dökülmesine olanak tanır ve öğrenmeyi pekiştirir.
Bu tür detayların eklenmesi, içeriği daha zengin ve öğretici hale getirecektir. Tekrar teşekkürler!
Bir üçgenin alanını hesaplarken yükseklik ve tabanı nasıl belirlemeliyim? Eşkenar üçgenle dik üçgenin alanını hesaplama yöntemleri arasında ne gibi farklar vardır?
Merhaba İzra,
Bir üçgenin alanını hesaplamak için taban ve yüksekliği belirlemeniz gerekir. Üçgenin alan formülü şöyledir: Alan = 1/2 taban yükseklik.
Eşkenar üçgende, tüm kenarlar eşit olduğu için yüksekliği bulmak biraz farklı olabilir. Önce tabanın yarısını alıp ve bu değeri kullanarak Pisagor teoremi ile yüksekliği hesaplayabilirsiniz. Dik üçgende ise, dik olan iki kenardan biri taban diğeri yükseklik olarak kullanılabilir.
Her iki üçgen tipi için de alan hesaplama yönteminde ana fark, yüksekliğin belirlenme şeklidir. Eşkenar üçgende yüksekliği bulmak için ek hesaplamalar gerekebilirken, dik üçgende bu daha basittir.
Umarım bu bilgiler yardımcı olur, iyi çalışmalar dilerim!
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?