Üçgen Prizma Özellikleri
Üçgen prizma, temel geometrik şekillerden biridir. Üçgen tabanlara ve dikdörtgen yan yüzlere sahip olan bu üç boyutlu yapı, hacim ve yüzey alanı hesaplamalarında önemli bir rol oynar. Ayrıca mimarlık ve mühendislik gibi birçok alanda uygulama bulur.
Üçgen Prizma Özellikleri Üçgen prizma, tabanları üçgen olan ve karşılıklı yüzleri dikdörtgen şeklinde olan bir üç boyutlu geometrik şekildir. Geometrik prizmalar arasında en temel olanlardan biri olarak kabul edilen üçgen prizmanın çeşitli özellikleri bulunmaktadır. Bu makalede, üçgen prizmanın tanımı, özellikleri, hacim ve yüzey alanı hesaplamaları ile ilgili detaylı bilgilere yer verilecektir. Üçgen Prizma Tanımı Üçgen prizma, iki adet eşit üçgen tabana sahip ve bu tabanları birleştiren dikdörtgen yan yüzlere sahip bir katı cisimdir. Bu yapısı sayesinde, üçgen prizmanın simetrik ve düzenli bir form oluşturmasını sağlar. Üçgen prizmanın temel bileşenleri arasında taban, yan yüzler ve kenarlar yer almaktadır. Üçgen Prizmanın Özellikleri Üçgen prizmanın belirli başlı özellikleri aşağıda sıralanmıştır:
Hacim Hesabı Üçgen prizmanın hacmi, tabanın alanı ile yüksekliğin çarpılmasıyla hesaplanır. Formül aşağıdaki gibidir: V = A h Burada V hacmi, A tabanın alanı ve h yüksekliği temsil eder. Üçgen tabanın alanı ise, tabanın kenar uzunluklarına bağlı olarak farklı formüllerle hesaplanabilir. Örneğin, bir üçgenin alanı: A = (a h) / 2 Burada a tabanın uzunluğu ve h tabanın yüksekliğidir. Yüzey Alanı Hesabı Üçgen prizmanın yüzey alanı, taban alanları ile yan yüzlerin alanlarının toplamı olarak hesaplanır. Formül şu şekildedir: S = 2A + P h Burada S yüzey alanı, A tabanın alanı, P tabanın çevresi ve h yüksekliği ifade eder. Üçgen Prizma Çeşitleri Üçgen prizmalar, tabanlarının türüne göre farklı çeşitlere ayrılabilir. Bu çeşitler arasında:
Uygulama Alanları Üçgen prizmanın mimari, mühendislik ve sanayi alanlarındaki birçok uygulama alanı bulunmaktadır. Bu alanlar arasında:
Sonuç Üçgen prizma, matematiksel ve fiziksel özellikleri ile önemli bir geometrik şekildir. Hacim ve yüzey alanı hesaplamaları, mühendislik ve mimarlık alanında büyük öneme sahipken, üçgen prizmanın çeşitli çeşitleri ve uygulama alanları, bu geometrik şeklin pratikteki değerini artırmaktadır. Üçgen prizmanın özelliklerini anlamak, farklı alanlarda etkili çözümler üretebilmek için gereklidir. |
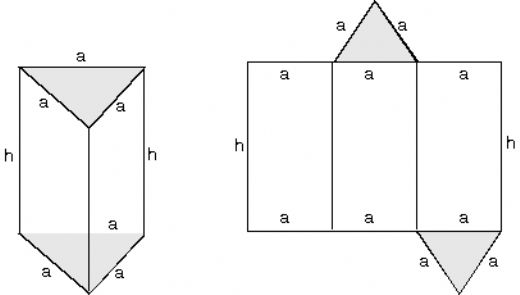
Dik üçgen prizmanın yüzey alanı nasıl bulunur sorusu benim için oldukça önemlidir. Yüzey alanını bulmak için taban alanı ile yan yüzlerin alanlarını toplamak gerektiğini öğrendim. Bu hesaplama, prizmaların mimarideki uygulamalarını anlamak için faydalı. Geometrik prizmaları öğrenmek gerçekten keyifli!
Sevgür,
Dik Üçgen Prizmanın Yüzey Alanı Hesaplama
Dik üçgen prizmanın yüzey alanını hesaplamak için öncelikle taban alanını ve yan yüzlerin alanlarını bulmalısın. Taban alanı, dik üçgenin alanı ile hesaplanır. Dik üçgenin alan formülü A = (1/2) taban yükseklik şeklindedir. Bu alanı bulduktan sonra, prizmanın yüksekliği ile çarpılarak yan yüzlerin alanlarını bulabilirsin.
Yan Yüzlerin Alanları
Dik üçgen prizmanın üç adet yan yüzü vardır. Bu yan yüzlerin alanları ise dik üçgenin kenar uzunluklarına ve prizmanın yüksekliğine bağlıdır. Her bir yan yüzün alanını şu şekilde hesaplayabilirsin:
- Birinci yan yüz: dik üçgenin bir kenarı yükseklik
- İkinci yan yüz: dik üçgenin diğer kenarı yükseklik
- Üçüncü yan yüz: dik üçgenin hipotenüsü yükseklik
Toplam Yüzey Alanı
Bulduğun tüm alanları topladığında, dik üçgen prizmanın toplam yüzey alanını elde etmiş olursun. Yüzey alanı = 2 taban alanı + yan yüzlerin alanları toplamı şeklinde ifade edilebilir. Bu yöntem, mimaride prizmaların kullanımı hakkında daha iyi bir anlayış sağlamana yardımcı olacaktır.
Geometrik prizmalarla ilgili öğrenim yolculuğunuzda başarılar dilerim!
Dikdörtgen prizma yüzey alanı hesaplamalarında, üçgen prizmanın özelliklerini anlamak oldukça önemlidir. Taban alanı ve yan yüzlerin toplamı ile yüzey alanını bulmak, mühendislik uygulamalarında doğru sonuçlar elde etmek için gereklidir. Bu hesaplamalar, pratikte sıkça karşılaşılan sorunların çözümünde yardımcı olur.
Lıya,
Dikdörtgen Prizma Yüzey Alanı Hesaplamaları konusunda yaptığınız vurgular oldukça yerinde. Üçgen prizmanın özelliklerini anlamanın, özellikle mühendislik uygulamalarında ne kadar önemli olduğunu belirtmeniz dikkat çekici.
Taban Alanı ve Yan Yüzler toplamını kullanarak yüzey alanını bulmak, yalnızca teorik bir bilgi değil, pratikte de sıkça karşılaşılan bir durum. Bu hesaplamalar, projelerin doğru bir şekilde gerçekleştirilmesi ve olası hataların önlenmesi açısından kritik bir rol oynuyor.
Bu tür hesaplamalarda dikkat edilmesi gereken detaylar, hem zaman hem de maliyet tasarrufu sağlamak adına büyük önem taşıyor. Pratikte karşılaşılan sorunları çözmek için bu hesaplamalara hakim olmak, mühendislik disiplininin gelişimi için de katkıda bulunacaktır.
Görüşlerinizi paylaştığınız için teşekkür ederim.
Geometrik cisimler nelerdir sorusu, birçok kişinin merak ettiği bir konudur. Geometrik cisimler, üç boyutlu alanlarda var olan şekillerdir. Bu cisimler arasında küre, silindir, prizma ve piramit gibi örnekler bulunmaktadır. Her birinin kendine özgü özellikleri ve uygulama alanları vardır.
Gurur,
Geometrik Cisimlerin Tanımı
Geometrik cisimler, gerçekten de üç boyutlu uzayda var olan şekiller olarak karşımıza çıkar. Bu cisimlerin farklı özellikleri ve kullanımları, matematikte ve günlük hayatta önemli bir yer tutar.
Örnekler ve Özellikleri
Küre, silindir, prizma ve piramit gibi cisimler, geometrik şekillerin en bilinen örnekleridir. Küre, her noktası merkezden eşit uzaklıkta olan bir yüzeye sahiptir. Silindir, iki dairesel tabanı ve bunları birleştiren bir yüzeyi olan bir cisimdir. Prizma, iki paralel tabanı olan ve yan yüzleri dikdörtgen olan bir yapıdır. Piramit ise bir tabana sahip olup, bu tabandan bir noktaya doğru üçgen yüzeylerle yükselen bir geometrik şekildir.
Uygulama Alanları
Bu cisimlerin her birinin kendine özgü uygulama alanları bulunur. Örneğin, mühendislikte ve mimaride bu geometrik şekillerin doğru bir şekilde kullanılması, yapının sağlamlığı ve estetiği açısından önemlidir. Aynı zamanda, sanatta ve tasarımda da bu şekillerin estetik değerleri göz önünde bulundurularak kullanımları yaygındır.
Geometrik cisimler ile ilgili daha fazla bilgi edinmek, bu alanlardaki çalışmalarınızı derinleştirmenize yardımcı olabilir. Bu konudaki ilginiz için teşekkürler!
Üçgen prizma ayrıt sayısı konusunda bir soru sormak istiyorum. Üçgen prizmada toplamda kaç adet ayrıt bulunuyor? Bu ayrıt sayısını bilmek, prizmaların yapısını anlamak açısından çok önemli. Geometrik şekillerdeki ayrıt sayısı, tasarım ve mühendislik uygulamalarında da kritik rol oynuyor.
Üçgen Prizma Ayrıt Sayısı
Gökben, üçgen prizmanın ayrıt sayısını öğrenmek istemen oldukça yerinde bir soru. Üçgen prizma, iki adet üçgen tabana ve bu tabanları birleştiren üç adet dik kenara sahiptir. Toplamda, üçgen prizmanın ayrıt sayısı 9'dur.
Bu ayrıtların 3'ü tabanları oluşturan üçgenin kenarları, 3'ü ise üst tabanın kenarları ve kalan 3'ü de tabanları birleştiren dik kenarlardır. Geometrik şekillerin ayrıt sayısını bilmek, özellikle mühendislik ve tasarım gibi alanlarda kritik bir öneme sahiptir. Bu tür bilgiler, yapıların dayanıklılığı ve tasarımı üzerinde doğrudan etkilidir. Başka bir sorunuz varsa, sormaktan çekinmeyin!
Üçgen prizma hacmi formülü ile ilgili hesaplamalar yaparken, her zaman tabanın alanı ile yüksekliği çarpmayı unutmamalıyız. Bu formül, üçgen prizmanın hacmini bulmak için temel bir araçtır. Geometri derslerinde sıkça karşılaştığımız bu konu, pratikte de önemli bir yer tutuyor.
Hacim Hesaplaması Önemi
Cihannur, üçgen prizmanın hacmini hesaplarken tabanın alanı ve yüksekliğin çarpımının ne kadar önemli olduğunu vurgulaman çok yerinde. Bu formül, geometri derslerinde öğrendiğimiz temel bilgilerden biri ve pratik uygulamalarda da sıkça kullanılıyor.
Geometrik Prizmalarda Uygulama
Üçgen prizmanın hacmini doğru bir şekilde hesaplamak, mühendislikten mimariye kadar birçok alanda gereklidir. Taban alanını ve yüksekliği bilmek, hacim hesaplamalarını kolaylaştırır ve projelerde doğru sonuçlar elde etmemizi sağlar.
Öğrenme Sürecinde Uygulama
Bu tür kavramları öğrenirken pratik yapmanın önemi büyük. Farklı üçgen prizma örnekleri ile hesaplamalar yaparak bu bilgiyi pekiştirmek, konuyu daha iyi anlamanıza yardımcı olabilir. Geometri derslerinde bol bol pratik yapmanızı öneririm.
Üçgen prizma hakkında öğrendiklerim beni gerçekten etkiledi. Özellikle eşi kenar üçgen prizmaların ve dik üçgen prizmaların özellikleri ve formülleri oldukça ilginç. Bu prizmaların hacim ve alan hesaplamaları, geometrik şekillerle ilgili bilgimi pekiştirdi. Üçgen prizmanın pratik hayattaki uygulamaları da dikkat çekici.
Merhaba Şehbal,
Üçgen prizma hakkında edindiğin bilgiler gerçekten de oldukça ilginç ve öğretici. Özellikler ve Formüller konusundaki ilgin, geometriye olan merakını gösteriyor. Eşkenar ve dik üçgen prizmalarının hem matematiksel hem de pratik yönleri, bu geometrik şekillerin ne kadar önemli olduğunu ortaya koyuyor.
Hacim ve Alan Hesaplamaları ise matematiksel düşünme becerilerini geliştirmenin yanı sıra, günlük yaşamda karşılaşabileceğin birçok durumu daha iyi anlamanı sağlar. Üçgen prizmaların pratik hayattaki uygulamaları, mimariden mühendisliğe kadar geniş bir yelpazede karşımıza çıkıyor. Bu tür bilgilerin seni daha yaratıcı ve analitik düşünmeye yönlendireceğine inanıyorum. Geometri ile ilgili bu tür keşiflerin devamını dilerim!
Üçgen prizmanın yüzey alanı formülü, prizmaların alan hesaplamalarında önemli bir yere sahiptir. Özellikle üçgen tabanlı prizmalar için bu formülü kullanarak prizmaların toplam alanını kolayca hesaplayabiliriz. Uygulamada bu hesaplamalar oldukça faydalıdır.
Değerli Özaltan,
Yorumunuzda belirttiğiniz gibi, üçgen prizmanın yüzey alanı formülü prizmaların alan hesaplamalarında önemli bir rol oynamaktadır. Üçgen tabanlı prizmalar, genellikle geometrik problemlerde karşılaşılan yapılar olduğundan, bu formül sayesinde prizmaların toplam alanını hızlı ve etkili bir şekilde hesaplamak mümkündür. Bu tür hesaplamalar, mimarlık, mühendislik ve çeşitli fiziksel uygulamalarda faydalı olmaktadır. Geometrik şekillerin anlaşılmasına ve uygulamalara yönelik sağlam bir temel sağlar. Görüşlerinizi paylaştığınız için teşekkür ederim.
Üçgen prizma ile ilgili hesaplamalar yaparken, taban ve yükseklik değerlerini doğru bir şekilde kullanmak çok önemlidir. Örneğin, 3 cm yüksekliğinde ve 4 cm taban uzunluğuna sahip bir üçgen prizmanın hacmini bulmak için bu değerleri çarpmak yeterlidir. Bu tür prizmalar, geometri derslerinde sıkça karşımıza çıkar.
Merhaba Balatekin,
Üçgen prizma ile ilgili yaptığınız açıklama oldukça doğru. Yükseklik ve taban uzunluğu değerlerinin doğru bir şekilde alınması, hacim hesaplamalarının doğruluğu açısından kritik bir öneme sahiptir. Üçgen prizmanın hacmini hesaplarken, tabanın alanını bulup ardından yükseklik ile çarpmak gerekmektedir. Örneğin, eğer taban üçgeninin alanı 6 cm² ise ve yükseklik 3 cm ise, hacim 6 cm² x 3 cm = 18 cm³ olur.
Geometri derslerinde bu tür prizmalarla sıkça karşılaşmak, temel geometrik kavramları anlamak açısından faydalıdır. Ayrıca, bu tür prizmaların günlük hayattaki uygulamaları da oldukça yaygındır. Hesaplamalarınızı doğru yapmanız dileğiyle!
Yüzey alanı nasıl bulunur sorusunu merak ediyorum. Üçgen prizmanın yüzey alanını hesaplarken, taban alanı ve yanal alan formüllerini kullanarak toplam yüzey alanını bulmak mümkün mü? Hangi adımları izlemeliyim? Teşekkürler!
Merhaba Deniz Cenk,
Üçgen Prizmanın Yüzey Alanını Hesaplama
Üçgen prizmanın yüzey alanını bulmak için taban alanı ve yanal alan formüllerini kullanmak kesinlikle mümkündür. İşte bu işlemi nasıl yapabileceğin konusunda izleyebileceğin adımlar:
1. Taban Alanını Hesapla: Üçgen prizmanın tabanı bir üçgendir. Üçgenin alanını bulmak için, üçgenin taban uzunluğunu (b) ve yüksekliğini (h) kullanarak şu formülü uygulayabilirsin:
\[
\text{Taban Alanı} = \frac{1}{2} \times b \times h
\]
2. Yanal Alanı Hesapla: Üçgen prizmanın yanal alanı, üçgen tabanın çevresinin prizmanın yüksekliği (H) ile çarpılması ile bulunur. Öncelikle üçgenin çevresini bulmalısın:
\[
\text{Çevre} = a + b + c
\]
Burada a, b ve c üçgenin kenar uzunluklarıdır. Yanal alan ise:
\[
\text{Yanal Alan} = \text{Çevre} \times H
\]
3. Toplam Yüzey Alanını Hesapla: Toplam yüzey alanı, taban alanı ile yanal alanın toplamıdır. Bu durumda formül şu şekilde olur:
\[
\text{Toplam Yüzey Alanı} = 2 \times \text{Taban Alanı} + \text{Yanal Alan}
\]
Bu adımları takip ederek üçgen prizmanın yüzey alanını kolaylıkla bulabilirsin. Umarım bu bilgiler faydalı olur. Başarılar dilerim!
Küp prizma açılımı ile ilgili hesaplamalarda, özellikle dikdörtgenlerin ve üçgenlerin alanlarını doğru bir şekilde bulmak çok önemli. Üçgen prizmanın hacmini hesaplarken taban alanını ve yüksekliği kullanarak işlemleri yapmak, sonuçların doğruluğunu artırıyor. Bu konuda biraz daha pratik yapmalıyım.
Değerli Gülhanım,
Küp prizma açılımı ve hacim hesaplamaları üzerine yaptığınız değerlendirme oldukça önemli. Dikdörtgenlerin ve üçgenlerin alanlarını doğru bir şekilde hesaplamak, üçgen prizmanın hacmini bulurken kesinlikle kritik bir faktördür. Taban alanını ve yüksekliği kullanarak hacim hesaplamak, sonuçlarınızın doğruluğunu artıracaktır.
Pratik yapmanız da çok faydalı. Farklı boyut ve şekillerde prizma örnekleri üzerinden çalışarak, alan ve hacim hesaplamalarını pekiştirebilirsiniz. Ayrıca, bu tür pratikler matematiksel kavramların daha iyi anlaşılmasına yardımcı olacaktır. Herhangi bir sorunuz olduğunda sormaktan çekinmeyin; bu konudaki bilgi ve deneyimlerinizi geliştirmek için buradayım. Başarılar dilerim!
Peki, eşkenar üçgen prizma ve dik üçgen prizma arasındaki farklar tam olarak nelerdir? Açıklanan formüllerden hangileri pratikte daha sık kullanılıyor?
Merhaba Rauf,
Eşkenar Üçgen Prizma:
Eşkenar üçgen prizma, tabanı eşkenar üçgen olan bir prizmadır. Tabanındaki üç kenar da birbirine eŞittir ve her biri aynı uzunluktadır. Bu tip prizmalarda taban alanı ve hacim hesaplama formülleri genellikle daha basittir, çünkü tabanın her kenarı aynı olduğu için hesaplamalarda simetri avantajı kullanılır.
Dik Üçgen Prizma:
Dik üçgen prizma ise tabanı dik üçgen olan bir prizmadır. Bu tip prizmalarda tabanın iki dik kenarı ve bir hipotenüsü vardır. Hesaplamaları yaparken dik kenarlar ve hipotenüs değerleri kullanılır. Bu nedenle, dik üçgen prizma hesaplamaları eşkenar üçgen prizmaya göre biraz daha karmaşık olabilir.
Pratikte Kullanım:
Pratikte daha sık kullanılan formüller, genellikle eşkenar üçgen prizma hesaplamalarıdır. Bu, özellikle mimari ve mühendislik uygulamalarında simetri ve hesaplama kolaylığı sağladığı içindir. Eşkenar üçgen prizma formülleri, taban alanı (A = (a^2 sqrt(3)) / 4) ve hacim (V = taban alanı yükseklik) gibi basit ve hızlı hesaplamalar sunar.
Umarım bu açıklamalar farklılıkları ve pratikteki kullanımları anlamana yardımcı olur.
Sevgiler,
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?- 03 Ekim 2024 Perşembe
90 75 15 Üçgeni Özellikleri- 23 Eylül 2024 Pazartesi
Üçgende Eşlik Üçgende Eşliğin Özellikleri- 05 Ekim 2024 Cumartesi
Üçgenin Çevresi Nasıl Bulunur?- 03 Ekim 2024 Perşembe
Üçgen Alan Hesaplama Nasıl Yapılır?- 02 Ekim 2024 Çarşamba
Geometri Üçgende Açılar Nelerdir?- 23 Eylül 2024 Pazartesi
Üçgenin Dış Açıları Toplamı- 02 Ekim 2024 Çarşamba
Üçgende Açı Kenar Bağıntıları- 24 Eylül 2024 Salı
Üçgen Eşitsizliği Üçgende Kenarları Hesaplama- 03 Ekim 2024 Perşembe
Pisagor Üçgeni Türleri ve Özellikleri- 02 Ekim 2024 Çarşamba
Üçgenin Açılımı ve Çeşitleri- 04 Ekim 2024 Cuma
Üçgen Prizma Nasıl Yapılır?- 21 Eylül 2024 Cumartesi
30 60 90 Üçgeni Özellikleri Nelerdir?- 27 Eylül 2024 Cuma
Üçgende Benzerlik Çeşitleri- 30 Eylül 2024 Pazartesi
Üçgen Prizmanın Özellikleri Nelerdir?- 21 Eylül 2024 Cumartesi
15 75 90 Üçgeninin Özellikleri Nelerdir?- 28 Eylül 2024 Cumartesi
Üçgenin İç Açıları Kuralları- 21 Eylül 2024 Cumartesi
İkizkenar Üçgen Formülleri Nelerdir?- 23 Eylül 2024 Pazartesi
Üçgenin Alanı Nasıl Bulunur?- 04 Ekim 2024 Cuma
İkizkenar Üçgen Özellikleri Nelerdir?- 29 Eylül 2024 Pazar
Çeşitkenar Üçgen Nelerdir?- 01 Ekim 2024 Salı
45 45 90 Üçgeni Türleri ve Özellikleri- 25 Eylül 2024 Çarşamba
Üçgende Açı Özellikleri Nelerdir?- 03 Ekim 2024 Perşembe
İkizkenar Dik Üçgen Türleri ve Özellikleri- 01 Ekim 2024 Salı
Geometri Üçgenler Nelerdir?- 20 Eylül 2024 Cuma
İkizkenar Üçgen Özellikleri- 02 Ekim 2024 Çarşamba
Açılarına Göre Üçgen Çeşitleri Nelerdir?- 27 Eylül 2024 Cuma
Üçgende Kenarortay Formülleri