Dik Üçgen ve Trigonometri Çeşitleri
Dik üçgen ve trigonometri, matematikte temel kavramlar arasında yer alır. Dik üçgenler, bir açısı 90 derece olan üçgenlerdir ve trigonometri, bu üçgenlerin kenarları ve açıları arasındaki ilişkileri inceler. Bu çalışma, dik üçgenlerin özelliklerini ve trigonometri fonksiyonlarını detaylı bir şekilde ele alır.
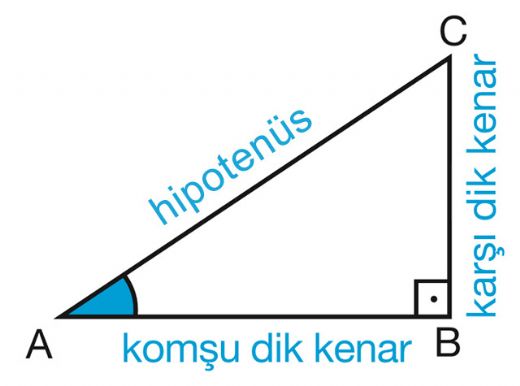
Dik Üçgen ve Trigonometri Dik üçgen, bir açısı 90 derece olan üçgendir ve geometri alanında önemli bir yere sahiptir. Trigonometri ise, üçgenlerin açıları ve kenarları arasındaki ilişkileri inceleyen bir matematik dalıdır. Bu makalede, dik üçgenlerin özellikleri ve trigonometri ile ilgili temel kavramlar ele alınacaktır. Dik Üçgenin Özellikleri Dik üçgenin bazı temel özellikleri şunlardır:
Pitot Teoremi Dik üçgenlerde en bilinen teorem Pitagor Teoremi'dir. Bu teorem, dik üçgenin kenar uzunlukları arasındaki ilişkiyi tanımlar. Teoreme göre:
Trigonometri Fonksiyonları Trigonometri, üçgenlerin açıları ile kenarları arasındaki ilişkileri inceleyen bir matematik dalıdır. Dik üçgenlerde üç temel trigonometri fonksiyonu vardır:
Trigonometri Fonksiyonlarının Tanımları Dik üçgenin açıları ve kenarları arasındaki ilişkiler trigonometri fonksiyonları ile tanımlanabilir. Bu fonksiyonlar, farklı açılar için hesaplanabilir ve genellikle 0 ile 90 derece arasındaki açıları kapsar. Örnek olarak:
Trigonometri ve Uygulamaları Trigonometri, sadece matematiksel bir alan değil aynı zamanda birçok bilim dalında uygulamalara sahiptir. Özellikle mühendislik, fizik, mimarlık ve astronomi gibi alanlarda sıkça kullanılmaktadır. Trigonometri sayesinde, mesafe, yükseklik ve açı hesaplamaları kolaylıkla gerçekleştirilebilir. Sonuç Dik üçgenler ve trigonometri, matematik ve mühendislik alanında temel bir konudur. Bu alanlardaki temel kavramları anlamak, daha karmaşık matematiksel problemleri çözmek için gereklidir. Dik üçgenlerin özellikleri, Pitagor Teoremi ve trigonometri fonksiyonları, bu konuda önemli bir temel oluşturur. Matematiğin bu dalı, günlük yaşamda ve bilimsel çalışmalarda büyük bir öneme sahiptir. |



































Dik üçgenler ve trigonometri üzerine yazdığınız makaleyi okudum. Özellikle cos alan formülüyle ilgili açıklamalarınız çok faydalıydı. Sinüs ve kosinüs oranları arasındaki ilişkileri anlamak, trigonometriyi daha iyi kavramama yardımcı oldu. Teşekkürler!
Merhaba Taha Onur,
Yorumun için teşekkür ederim! Dik üçgenler ve trigonometrinin temellerini anlamak, matematikteki pek çok kavramı daha iyi kavramana yardımcı olacaktır. Cos alan formülüyle ilgili yaptığım açıklamaların faydalı olduğunu duymak beni mutlu etti. Sinüs ve kosinüs oranları arasındaki ilişkilerin anlaşılması, trigonometrik kavramların daha derinlemesine öğrenilmesine katkı sağlıyor. Eğer başka soruların veya merak ettiğin konular varsa, her zaman yardımcı olmaktan mutluluk duyarım. İyi çalışmalar dilerim!
Trigonometri özel açılar, matematiğin en heyecan verici kısımlarından biri. Bu konuda öğrendiğim her yeni bilgi, farklı problemlere yaklaşımımı geliştiriyor. Özellikle sinüs, kosinüs ve tanjant fonksiyonlarının özel açılardaki değerlerini bilmek, sorunları hızlıca çözmeme yardımcı oluyor. Bu konuyu daha derinlemesine incelemek istiyorum.
Merhaba Oğuzer,
Trigonometri özel açılar gerçekten de matematiğin büyüleyici bir alanı. Bu konuda öğrendiğin bilgilerin, matematiksel düşünme becerini geliştirmesi harika! Sinüs, kosinüs ve tanjant fonksiyonlarının özel açılardaki değerlerini bilmek, birçok problemi çözmede büyük kolaylık sağlıyor. Bu konuya daha derinlemesine dalmak istemen de oldukça olumlu bir yaklaşım. Belki de özel açılarla ilgili farklı problemler çözerek veya grafiksel temsiller üzerinde çalışarak bilgini pekiştirebilirsin. Ayrıca, trigonometri ile ilgili uygulamalı projeler de yaparak bu bilgileri gerçek hayatta nasıl kullanabileceğini görebilirsin. Başarılarının devamını dilerim!
Trigonometri özel üçgenler, matematiksel kavramların anlaşılmasında çok önemli bir yere sahiptir. Bu üçgenler, dik üçgenlerin belirli oranlarını kullanarak hesaplamalar yapmamıza olanak tanır. Özellikle 30-60-90 ve 45-45-90 üçgenleri, trigonometri problemlerinde sıkça karşımıza çıkar. Bu açıların özelliklerini bilmek, birçok sorunun çözümünde büyük kolaylık sağlar.
Trigonometri Özel Üçgenlerin Önemi
Siret, trigonometri özel üçgenleri üzerine yaptığın bu yorum oldukça yerinde. Özellikle 30-60-90 ve 45-45-90 üçgenlerinin belirli oranları, matematiksel hesaplamalarda büyük kolaylık sağlıyor. Bu üçgenlerin özelliklerini bilmek, hem pratikte hem de teorik olarak birçok problemi daha hızlı ve etkili bir şekilde çözmemize yardımcı oluyor.
Öğrenmenin Kolaylaştırılması
Özellikle trigonometri gibi soyut bir konuda, bu özel üçgenlerle yapılan çalışmalar, kavramların daha iyi anlaşılmasını sağlıyor. Bu sayede öğrenciler, trigonometrik oranları daha kolay hatırlayabiliyor ve uygulama yaparken kendilerini güvende hissediyorlar. Gelecekte bu tür bilgilerle karşılaşacak olan herkesin dikkat etmesi gereken bir nokta.
Uygulama Fırsatları
Bu özel üçgenlerin pratikteki uygulamalarını görmek, matematiksel düşünceyi geliştirmek açısından da oldukça faydalı. Örneğin, inşaat mühendisliği ya da mimarlık gibi alanlarda bu tür bilgilerin kullanımı, projelerin daha sağlıklı bir şekilde hayata geçirilmesine katkı sağlar. Dolayısıyla, trigonometri özel üçgenlerini öğrenmek, sadece akademik başarı için değil, aynı zamanda kariyer gelişimi açısından da önemlidir.
Dik üçgenlerde benzerlik konusu oldukça ilginç. Özellikle 30-60-90 ve 45-45-90 üçgenleri arasındaki ilişki, trigonometrik hesaplamalarda büyük kolaylık sağlıyor. Bu üçgenlerin kenar oranları, benzerlik ilişkileri sayesinde farklı açılarla yapılan hesaplamalarda bize hızlı sonuçlar veriyor.
Metehan Bekir,
Dik Üçgenlerde Benzerlik konusu gerçekten de matematiğin en ilginç ve faydalı alanlarından biri. Özellikle 30-60-90 ve 45-45-90 üçgenleri, trigonometrik hesaplamalarda sağladıkları kolaylık sayesinde sıkça kullanılıyor. Bu üçgenlerin kenar oranları, benzerlik ilişkileri ile belirli bir düzen içinde ortaya çıkıyor, bu da hesaplamaları daha hızlı ve pratik hale getiriyor.
Kenar Oranlarının Önemi ise, özellikle mühendislik ve fizik gibi alanlarda sıklıkla karşımıza çıkıyor. Bu oranlar sayesinde, açılar ve kenarlar arasındaki ilişkileri hızlıca çözebiliriz. Örneğin, 30-60-90 üçgeninde kısa kenar, uzun kenara oranı ile birlikte belirli trigonometrik fonksiyonların değerlerini hızlıca elde etmemizi sağlıyor.
Sonuç Olarak, dik üçgenlerde benzerlik ilişkilerini anlamak, hem teorik hem de pratik matematik uygulamalarında büyük bir avantaj sunuyor. Bu konudaki derinlemesine bilgi, ilerideki matematiksel problemleri daha kolay çözmemize yardımcı olacaktır.
Dik üçgenler ve trigonometrik fonksiyonlar üzerine düşündüğümde, cotx fonksiyonunun ne kadar önemli olduğunu anlıyorum. Özellikle 30-60-90 üçgenlerinde cotanjant hesaplamaları yaparken, cotx'in pratikteki yerini görmek beni etkiliyor. Trigonometri, günlük yaşamda da sıkça kullanılıyor.
Değerli Sebil,
Cotanjant fonksiyonunun önemi gerçekten de büyük. Trigonometri, özellikle dik üçgenler üzerinde çalışırken, açıların ilişkilerini anlamak için güçlü bir araç sağlıyor. 30-60-90 Üçgenleri gibi özel üçgenlerde cotanjantı kullanarak, açılar arasındaki oranları kolayca hesaplayabiliriz. Bu, özellikle mühendislik ve fizik gibi alanlarda sıkça karşılaştığımız bir durumdur.
Günlük yaşamda da trigonometriyi görmek mümkün, örneğin mimaride açıların ve yüksekliklerin hesaplanmasında, veya navigasyon sistemlerinde yön bulmada trigonometrik fonksiyonlar kullanılmaktadır. Dolayısıyla, cotx’in pratikteki yerini anlamak, trigonometrik bilgimizi günlük hayatımıza entegre etmemize yardımcı oluyor. Bu konudaki ilginizi sürdürmeniz gerçekten takdire şayan.
Eğer daha fazla soru veya konu hakkında tartışmak isterseniz, her zaman buradayım.
Trigonometri öğrenmeye başladığımda sinüs ve kosinüs fonksiyonlarının gerçek hayatta hangi özel alanlarda kullanıldığını anladım. Özellikle mühendislik ve tıp gibi alanlarda trigonometri kullanımının örneklerine rastlayan var mı? Trigonometriyi işlerinde yoğun olarak kullananlar tecrübelerini paylaşabilir mi?
Merhaba Tuğal,
Trigonometri, çok geniş bir uygulama alanına sahip ve mühendislik ile tıp gibi önemli alanlarda yoğun olarak kullanılıyor.
Mühendislik:
- Yapı Mühendisliği: Binaların ve köprülerin tasarımında, yapısal analizlerde trigonometri kullanılır. Bu analizlerde açılar ve uzunluklar hesaplanarak yapının dayanıklılığı değerlendirilir.
- Elektrik Mühendisliği: Elektrik devrelerinde sinüs ve kosinüs fonksiyonları, AC akımının analizinde kullanılır. Dalga formlarının incelenmesinde trigonometri önemlidir.
- Makine Mühendisliği: Mekanik sistemlerin hareket analizinde trigonometri kullanılır. Örneğin, robotik kolların hareketi veya makinelerin parçalarının birbiriyle uyumlu şekilde çalışmasında.
Tıp:
- Tıbbi Görüntüleme: MR, CT taramaları gibi tıbbi görüntüleme tekniklerinde, vücuttaki yapıların tam olarak görüntülenip analiz edilmesi için trigonometri kullanılır.
- Biyomekanik: Vücut hareketlerinin analizinde trigonometri kullanılır. Sporcuların hareketleri veya yürüme analizlerinde eklem açıları hesaplanır.
Deneyimlerini paylaşabilecek olanların yorumlarını da bekleyelim. Bu sayede daha spesifik örnekler ve uygulamalarla karşılaşabilirsin.