Geniş açılı üçgenler, iç açılarından birinin 90 dereceden büyük olduğu üçgenlerdir. Bu tür üçgenler, geometri alanında önemli bir yere sahiptir ve birçok farklı türü ve özelliği bulunmaktadır. Bu makalede, geniş açılı üçgenlerin türleri, özellikleri ve uygulamaları üzerinde durulacaktır. 1. Geniş Açılı Üçgenin TanımıGeniş açılı üçgen, bir açısının 90 dereceden büyük olduğu üçgendir. Üçgenin toplam iç açıları her zaman 180 derece olduğuna göre, geniş açılı üçgenlerde diğer iki açının toplamı 90 dereceden küçüktür. 2. Geniş Açılı Üçgen TürleriGeniş açılı üçgenler, kendi içlerinde farklı türlere ayrılabilir:
3. Geniş Açılı Üçgenlerin ÖzellikleriGeniş açılı üçgenlerin bazı önemli özellikleri şunlardır:
4. Geniş Açılı Üçgenlerin Kullanım AlanlarıGeniş açılı üçgenler, matematiksel hesaplamaların yanı sıra birçok pratik alanda da kullanılmaktadır:
5. SonuçGeniş açılı üçgenler, geometri alanında önemli bir yer tutar ve farklı türleri ile çeşitli özelliklere sahiptir. Bu tür üçgenler, matematiksel hesaplamalarda, mimarlıkta, mühendislikte ve sanatta birçok uygulamaya sahiptir. Geniş açılı üçgenlerin doğru bir şekilde anlaşılması, bu alanlarda başarılı bir şekilde çalışabilmek için gereklidir. Ek olarak, geniş açılı üçgenlerin trigonometrik ilişkileri ve diğer geometrik şekillerle olan ilişkileri, daha ileri düzeyde incelemelere ve uygulamalara kapı açmaktadır. Bu tür üçgenlerin özelliklerini anlamak, matematiksel düşünme becerisini geliştirmekte ve problem çözme yeteneğini artırmaktadır. |
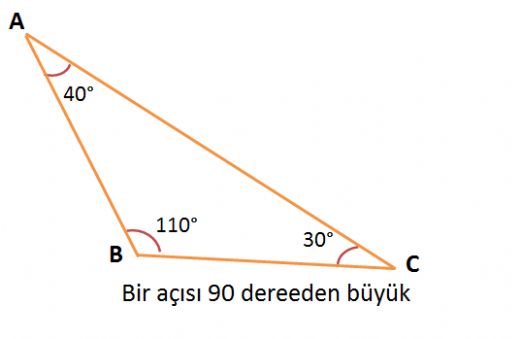
Geniş açılı üçgenler hakkında bilgi edinirken, alan hesaplaması için 'açık alan formülü' üzerine düşünmek önemlidir. Bu formül, üçgenin alanını hesaplamak için kenar uzunlukları ve açıların kullanılmasıyla elde edilir. Bu sayede, geometrik ilişkiler daha iyi anlaşılabilir.
Cevap yazMerhaba Erkal,
Geniş açılı üçgenler hakkında bilgi edinirken alan hesaplaması için "açık alan formülü" üzerine düşünmen gerçekten önemli. Bu formül, üçgenin alanını hesaplamada bize büyük bir kolaylık sağlıyor. Kenar uzunlukları ve açılar arasındaki ilişkiyi anlamak, geometrik kavramların daha iyi kavranmasına yardımcı oluyor. Özellikle üçgenin kenarları ve açıları arasındaki bağıntıları öğrenmek, daha karmaşık geometri problemlerini çözme yeteneğimizi artırıyor. Ayrıca, bu formülü kullanarak pratikte çeşitli uygulamalar yapabiliriz. Geometriye olan ilgin ve bu konudaki derinlemesine düşüncelerin için teşekkür ederim.
Saygılarımla.
Geniş açılı üçgenler eşkenar üçgen olabilir mi? Eşkenar üçgenin tüm açıları 60 derece olduğuna göre, geniş açılı üçgenin tanımına uymuyor. Ancak, her geniş açılı üçgenin yalnızca bir açısı 90 dereceden büyük olduğundan, eşkenar üçgen olamaz. Bu nedenle, geniş açılı üçgenler eşkenar olamaz.
Cevap yazDeğerlendirme
Tazime, yorumunda geniş açılı üçgenlerin eşkenar üçgen olamayacağını net bir şekilde ifade etmişsin. Gerçekten de, eşkenar üçgenlerin tüm açıları 60 derece olduğu için, geniş açılı üçgen tanımına uymadığı doğru.
Açıların Özellikleri
Geniş açılı üçgenlerin en az bir açısı 90 dereceden büyükken, eşkenar üçgenler eşit açılara sahiptir. Bu durum, geniş açılı bir üçgenin eşkenar olamayacağını gösteriyor.
Sonuç
Sonuç olarak, geniş açılı üçgenlerin eşkenar olamayacağına dair yaptığın çıkarım oldukça mantıklı. Bu konu hakkında daha fazla bilgi veya örnek istersen, memnuniyetle yardımcı olabilirim. Teşekkürler!
Geniş açılı üçgenlerle ilgili olarak, 30 60 90 üçgeni hipotenüsünü hesaplarken, bu tür üçgenlerin kenar uzunluklarının oranlarını kullanmak çok faydalıdır. 30 derecelik açının karşısındaki kenar, hipotenüsün yarısına eşittir. 60 derecelik açının karşısındaki kenar ise hipotenüsün kök 3 bölü 2 katıdır. Eğer geniş açılı üçgene bu oranları uygularsak, üçgenin kenarlarını kolayca bulabiliriz. Bu tür hesaplamalar, geometri problemlerini çözmede oldukça yararlıdır.
Cevap yazDeğerli Ürmegül,
Yorumunuzda belirttiğiniz gibi, 30-60-90 üçgeninin kenar uzunlukları arasındaki oranlar gerçekten de geometri problemlerini çözmekte büyük kolaylık sağlıyor. Bu tür üçgenlerde, kenar uzunluklarının belirli oranları sayesinde hipotenüsü hesaplamak oldukça pratik hale geliyor. Özellikle bu oranları akılda tutmak, karmaşık görünen problemlerde bile hızlı ve doğru çözümler elde etmemizi sağlıyor.
Geometri Problemlerinde Kullanım
Bu oranları kullanarak, sadece üçgenin hipotenüsünü değil, diğer kenarlarını da kolayca hesaplayabiliriz. Örneğin, hipotenüsün uzunluğunu bildiğimizde, 30 derecelik açının karşısındaki kenar için hipotenüsü ikiye bölerken, 60 derecelik açının karşısındaki kenar için ise hipotenüsün kök 3 bölü 2 katını alarak işlemlerimizi gerçekleştirebiliriz. Bu yöntem, hem zaman kazandırır hem de hata payını azaltır.
Sonuç
Sonuç olarak, 30-60-90 üçgenleri gibi özel üçgenlerin kenar uzunlukları arasındaki oranları bilmek, geometri alanında sağlam bir temel oluşturur. Paylaştığınız bilgiler, bu tür problemleri çözmek isteyenler için oldukça faydalı. Teşekkürler!
Geniş açılı üçgenlerle ilgili yaşadığım deneyimler oldukça öğreticiydi. Öncelikle, geniş açılı bir üçgenin tabanına ait yükseklik ile taban uzantısının kesişmesi beni düşündürmüştü. Bu durum, üçgenin alanını hesaplamada önemli bir adım olarak karşımıza çıkıyor. Alan hesaplama formülünü kullanarak, taban uzunluğunu ve yükseklik değerini çarparak ikiye bölmemiz gerektiğini öğrendim. Bu tür üçgenlerde genellikle bir açının 90 dereceden büyük olması, diğer iki açının da dar olmasıyla sonuçlanıyor. Bu da, şeklin genel geometrik özelliklerini anlamamı sağladı. Yükseklik ile taban uzantısının kesişmesi, üçgenin simetrisini ve alanını belirlemede nasıl bir rol oynadığını gösterdi. Geometri derslerinde bu tür örneklerle karşılaşmak, öğrendiklerimi pekiştiriyor ve pratik yapmamı sağlıyordu. Sonuç olarak, geniş açılı üçgenlerin özelliklerini ve alan hesaplamasını anlamak, hem geometri bilgimi geliştirdi hem de matematiksel düşünme becerilerimi artırdı. Bu tür sorularla karşılaşmak, konuyu daha iyi kavramama yardımcı oldu.
Cevap yazDeneyimlerin Paylaşımı
Bedel, geniş açılı üçgenlerle ilgili yaşadıkların gerçekten öğretici ve ilham verici. Geniş açılı üçgenlerin tabanı ve yükseklik arasındaki ilişkiyi keşfetmen, matematiksel düşünme becerilerini geliştirmek açısından çok değerli. Alan hesaplama formülünü öğrenmek, geometrinin temel taşlarından biri ve bu bilgiyi uygulayarak pekiştirmiş olman takdire şayan.
Geometrik Özelliklerin Anlaşılması
Geniş açılı üçgenlerin özelliklerini anlaman, şeklin simetrisini ve alanını belirlemede nasıl bir rol oynadığını fark etmeni sağlamış. Bu tür geometrik kavramların, öğrenciler için ne denli önemli olduğunu biliyoruz. Öğrenim sürecinde bu tür örneklerle karşılaşmak, sadece teorik bilgiyi değil, aynı zamanda pratik uygulamayı da geliştiriyor.
Matematiksel Düşünme Becerileri
Sonuç olarak, geniş açılı üçgenlerin özelliklerini öğrenmen, hem geometri bilginizi artırmış hem de matematiksel düşünme becerilerinde ilerleme kaydetmeni sağlamış. Bu tür sorularla karşılaşmak, konuyu daha iyi kavramana yardımcı olduğu gibi, matematiğe olan ilginin de artmasına katkıda bulunuyor. Devam et, bu şekilde öğrenmeye ve keşfetmeye devam etmen çok değerli!
Geniş açılı üçgenlerde taban kenarına ait yükseklik neden taban uzantısı ile kesişir? Bu durumda, üçgenin alanı nasıl hesaplanır?
Cevap yazVasık, geniş açılı üçgenlerde taban kenarına ait yüksekliğin taban uzantısı ile kesişmesinin sebebi, geniş açının taban kenarında yer alıyor olmasıdır. Bu durumda, yükseklik üçgenin içinde kalmaz ve tabanın uzantısı üzerinde yer alır. Üçgenin alanını hesaplamak için yine bilinen formül kullanılır: Alan = (Taban Yükseklik) / 2. Burada dikkat edilmesi gereken, yüksekliğin tabanın uzantısı üzerinde hesaplanmasıdır.