30 60 90 Üçgeni Özellikleri Nelerdir?

30-60-90 üçgeni, trigonometri ve geometri açısından önemli bir özel dik üçgendir. 30, 60 ve 90 derece açıları ile tanımlanan bu üçgenin kenar uzunlukları belirli bir orantıdadır. Alan ve çevre hesaplamalarında da pratik uygulamalara olanak tanır.

Konu kakkında 1 soru soruldu ve cevaplandı

30 60 90 üçgeni, trigonometri ve geometri alanında önemli bir yere sahip olan özel bir dik üçgendir. Bu üçgenin köşe açıları, 30 derece, 60 derece ve 90 derece olarak belirlenmiştir. Aşağıda, 30 60 90 üçgeninin temel özellikleri detaylı bir şekilde ele alınmaktadır.

1. Açı Özellikleri

30 60 90 üçgeninin açılarının özellikleri, bu üçgenin temel özelliklerini anlamak için kritik öneme sahiptir.

Bir açısı 30 derece, diğeri 60 derece ve üçüncü açısı ise 90 derecedir.
30 derecelik açı, dik kenarın karşısındadır ve en küçük açıdır.
60 derecelik açı, 30 derecelik açının komşusudur ve orta büyüklükte bir açıdır.
90 derecelik açı, üçgenin dik açısıdır ve en büyük açıdır.

2. Kenar Uzunlukları

30 60 90 üçgeninin kenar uzunlukları, açıları ile belirli bir orantı içerisindedir. Bu oranlar, üçgenin matematiksel özelliklerini anlamak için hayati öneme sahiptir.

30 derecelik açının karşısındaki kenar (k) en kısa kenardır ve bu kenarın uzunluğu "k" birimdir.
60 derecelik açının karşısındaki kenar, 30 derecelik açının karşısındaki kenarın √3 katıdır (k√3 birim).
90 derecelik açının karşısındaki kenar, 30 derecelik açının karşısındaki kenarın 2 katıdır (2k birim).

3. Alan ve Çevre Hesaplamaları

30 60 90 üçgeninin alanı ve çevresi, kenar uzunlukları kullanılarak kolaylıkla hesaplanabilir.

Bir üçgenin alanı, temel kenar yüksekliğin çarpımı ile 1/2 oranına göre hesaplanır. 30 60 90 üçgeni için alan A = (k k√3) / 2 = (k²√3)/2 birim karedir.
Çevre ise, üçgenin tüm kenarlarının toplamıdır. Çevre C = k + k√3 + 2k = k(3 + √3) birimdir.

4. Trigonometric Fonksiyonlar

30 60 90 üçgeninin açıları, trigonometri açısından da özel değerler taşır. Bu üçgenin açıları ile ilgili trigonometrik fonksiyonlar aşağıda belirtilmiştir.

sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = 1/√3
sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3
sin(90°) = 1, cos(90°) = 0, tan(90°) tanımsızdır.

5. Uygulama Alanları

30 60 90 üçgeni, birçok alanda uygulama alanı bulur. Bu üçgenin özellikleri, pratikte ve teoride farklı amaçlar için kullanılmaktadır.

Mimari tasarımlarda, özellikle çatı yapılarında bu üçgenin özellikleri sıklıkla kullanılır.
Fiziksel problemler ve mühendislik hesaplamalarında, bu üçgenin trigonometri fonksiyonları önemli rol oynar.
Matematiksel problemlerin çözümünde, 30 60 90 üçgeninin kenar ve açı ilişkileri, karmaşık hesaplamaları basitleştirmektedir.

Sonuç olarak, 30 60 90 üçgeni, matematik ve mühendislik alanında önemli bir yere sahip olan özel bir üçgendir. Açıları ve kenar uzunlukları arasındaki orantılar, bu üçgenin belirgin özelliklerini oluşturur. Bu özellikler, hem teorik hem de pratik uygulamalarda yaygın olarak kullanılmaktadır.

Yeni Soru Sor / Yorum Yap

Sizden Gelen Sorular / Yorumlar

Özgür 21 Temmuz 2024 Pazar

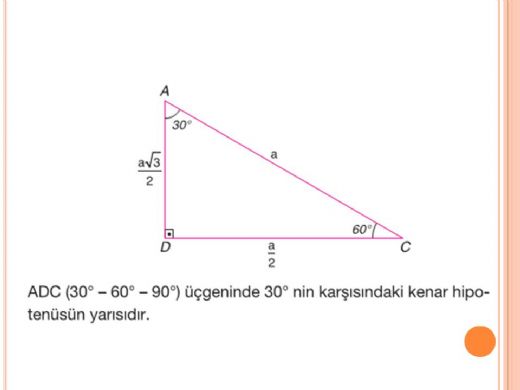
Acaba 30 60 90 üçgeninin hipotenüsünü hesaplamada neden 30 derecenin karşısındaki kenar uzunluğunun 2 katını alıyoruz? Bu kuralın mantığı nedir?

Admin 21 Temmuz 2024 Pazar

Merhaba Özgür,

30-60-90 üçgeni özel bir üçgendir ve bu üçgenin kenar uzunlukları arasında belirli bir oran vardır. Bu üçgende 30 derecelik açının karşısındaki kenar "a" ise, hipotenüs bu kenarın 2 katıdır, yani 2a. Bunun sebebi, 30-60-90 üçgeninin bir eşkener üçgenin iki eşit parçaya bölünmesiyle oluşmasıdır. Eşkener üçgende tüm kenarlar eşit olduğu için, bu iki parçadan biri 30 derece olur ve hipotenüs de eşkener üçgenin bir kenarının uzunluğuna eşit olur, yani 2a olur.

Umarım açıklayabilmişimdir.