
İkizkenar Üçgen Özellikleri
İkizkenar üçgenler, geometrinin temel yapı taşlarından biridir ve simetri özelliği ile dikkat çeker. İki kenarının eşit uzunlukta olması, çeşitli alanlarda kullanımını sağlar. Bu yazıda, ikizkenar üçgenlerin özellikleri, alan hesaplama yöntemleri ve uygulama alanları ele alınmaktadır.
İkizkenar Üçgen Özellikleri İkizkenar üçgen, geometrinin temel şekillerinden biridir. İkizkenar üçgen, iki kenarının eşit uzunlukta olduğu ve bu kenarları arasında kalan açının, diğer açıdan farklı olduğu bir üçgendir. Bu makalede, ikizkenar üçgenin özellikleri, formülleri ve kullanım alanları detaylı bir şekilde ele alınacaktır. İkizkenar Üçgenin Tanımı İkizkenar üçgen, en az iki kenarı eşit uzunlukta olan bir üçgendir. İkizkenar üçgenin temel özellikleri arasında, eşit kenarların karşısında yer alan açıların eşit olması bulunmaktadır. Bu durum, ikizkenar üçgenin simetrik bir yapıya sahip olduğunu gösterir. İkizkenar Üçgenin Özellikleri İkizkenar üçgenin birçok önemli özelliği bulunmaktadır:
İkizkenar Üçgenin Alanı İkizkenar üçgenin alanı, taban uzunluğu ve yüksekliği kullanılarak hesaplanabilir. Alan formülü aşağıdaki gibidir:\[ \text{Alan} = \frac{1}{2} \times \text{Taban} \times \text{Yükseklik} \]Ayrıca, kenar uzunlukları verilmişse, alan Heron formülü kullanılarak da hesaplanabilir. Kenar uzunlukları \( a \) ve \( b \) eşit olduğunda, üçgenin alanı şu şekilde hesaplanabilir:\[ \text{Alan} = \frac{b}{4} \sqrt{4a^2 - b^2} \] İkizkenar Üçgenin Kullanım Alanları İkizkenar üçgenler, matematik ve geometri alanlarının yanı sıra mühendislik, mimarlık ve sanat gibi birçok alanda da kullanılmaktadır. Özellikle:
Sonuç İkizkenar üçgen, geometrinin temel yapı taşlarından biri olarak, birçok özelliği ve kullanım alanıyla dikkat çekmektedir. Eşit kenarları ve açılarının sağladığı simetri, bu üçgenin matematiksel ve estetik açıdan önemini artırmaktadır. İkizkenar üçgenler, sadece teorik bir kavram değil, aynı zamanda pratikte de sıkça kullanılan bir geometrik şekildir. Bu nedenle, ikizkenar üçgenlerin özelliklerini ve kullanım alanlarını bilmek, matematiksel düşünme becerilerini geliştirmek için büyük bir katkı sağlamaktadır. |
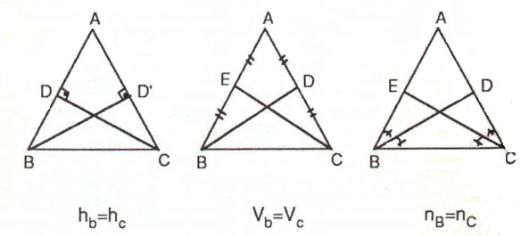















































İkizkenar üçgende tepe noktasından tabana indirilen dikmenin hem kenarortay, hem açıortay, hem de yükseklik görevini gördüğünden bahsediliyor. Peki, bu özelliği kullanarak bir soruyu çözerken nelere dikkat etmeliyiz? Bu dikmenin tabanı iki eşit parçaya böldüğünü nasıl hesaba katmalıyız?
Eryalçın,
İkizkenar Üçgende Özellikler
İkizkenar üçgenlerde, tepe noktasından tabana inen dikme, üçgenin simetrik yapısından dolayı birçok önemli özelliği taşır. Bu dikme, hem kenarortay hem de yükseklik görevi gördüğü için, soruları çözerken bu özellikleri dikkate almak oldukça önemlidir.
Dikkat Edilmesi Gerekenler
1. Dikmenin Konumu: Dikmenin, tepe noktasından tabana inmesi, üçgenin simetrik yapısını korur. Bu nedenle, dikmenin tabanı iki eşit parçaya böldüğünü unutmamalısınız.
2. Açı ve Kenar Orantıları: Bu dikmenin oluşturduğu açıların ve kenarların oranlarını kullanarak, çeşitli trigonometrik ilişkileri uygulayabilirsiniz. Özellikle, eşit kenar uzunlukları ve açıların varlığını göz önünde bulundurmalısınız.
3. Alan Hesabı: İkizkenar üçgenin alanını hesaplamak için tabanı ve yüksekliği kullanarak, alan formülünden yararlanabilirsiniz. Dikmenin tabanı iki eşit parçaya böldüğünden, her bir parçanın alanını ayrı ayrı hesaplamak yerine, toplam alanı direkt bulmak daha pratik olacaktır.
Sonuç Olarak
Dikmenin, üçgenin simetrik yapısı sayesinde sağladığı bu özellikleri kullanmak, soruların çözümünde büyük kolaylık sağlar. Soruları çözerken bu özellikleri kullanarak daha etkili ve hızlı sonuçlar elde edebilirsiniz.