
Eşkenar Üçgenin Alanı
Eşkenar üçgen, kenar uzunlukları eşit olan ve iç açıları 60 derece olan bir geometrik şekildir. Alan hesaplamasında kullanılan formüller ve yöntemler, öğrencilerin temel matematik bilgilerini pekiştirmelerine yardımcı olur. Bu yazıda, eşkenar üçgenin alanını hesaplama yöntemleri ele alınmaktadır.
Eşkenar Üçgenin Alanı Eşkenar üçgen, kenar uzunlukları birbirine eşit olan bir üçgendir ve iç açılarının her biri 60 derecedir. Eşkenar üçgenin alanını hesaplamak için farklı yöntemler bulunmaktadır. Bu makalede, eşkenar üçgenin alanının nasıl hesaplandığına dair detaylı bir inceleme yapılacaktır. Eşkenar Üçgenin Tanımı Eşkenar üçgen, aşağıdaki özelliklere sahip bir üçgendir:
Eşkenar üçgenler, geometri ve trigonometri alanında önemli bir yere sahiptir. Özellikle simetrik yapıları sayesinde birçok matematiksel problemde kullanılırlar. Eşkenar Üçgenin Alanının Hesaplanması Eşkenar üçgenin alanını hesaplamak için en yaygın yöntem, kenar uzunluğuna dayanmaktadır. Eşkenar bir üçgenin alanı, aşağıdaki formülle hesaplanabilir:
Burada, A eşkenar üçgenin alanını, a ise kenar uzunluğunu temsil etmektedir. Bu formül, eşkenar üçgenin alanını bulmak için basit ve etkilidir. Örnek Hesaplama Örneğin, kenar uzunluğu 6 cm olan bir eşkenar üçgenin alanını hesaplayalım.
Bu durumda, eşkenar üçgenin alanı yaklaşık olarak 15.59 cm² olacaktır. Eşkenar Üçgenin Alanını Bulmanın Alternatif Yöntemleri Eşkenar üçgenin alanını bulmanın başka yöntemleri de vardır:
Sonuç Eşkenar üçgenler, matematikte ve geometri derslerinde önemli bir yer tutmaktadır. Alanlarının hesaplanması için farklı yöntemlerin olması, bu geometrik şeklin esnekliğini ve kullanım kolaylığını artırmaktadır. Eşkenar üçgenin alanını bulmak, yalnızca matematiksel bir uygulama değil, aynı zamanda günlük hayatta da karşımıza çıkan pratik bir işlemdir. Bu nedenle, eşkenar üçgenin alanı ile ilgili temel bilgilerin öğrenilmesi, öğrenciler için büyük önem taşımaktadır. Ek Bilgiler Eşkenar üçgenler, birçok mühendislik ve mimari tasarımda da sıkça kullanılan bir yapı elemanıdır. Bu yapılar, yüksek dayanıklılıkları ve estetik görünümleri ile bilinir. Ayrıca, eşkenar üçgenin simetrik yapısı, onu çeşitli sanatsal ve dekoratif uygulamalarda da popüler kılmaktadır. Geometri ve matematik derslerinde, eşkenar üçgenler sıkça karşılaşılan bir konudur ve çeşitli problemlerle öğrencilerin bu konudaki becerilerini geliştirmeleri sağlanmaktadır. |
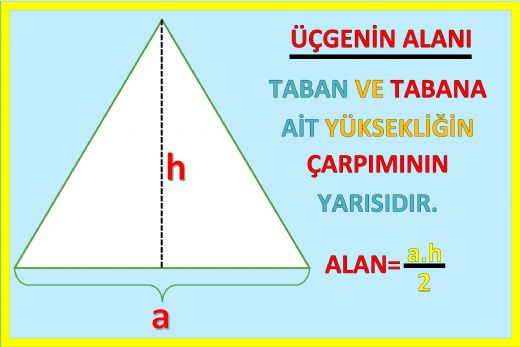





























Eşkenar üçgenin alanını hesaplamak için en etkili yöntemlerden biri yükseklik kullanarak yapılır. Yüksekliği bularak A = (1/2) a h formülünü uygulamak, üçgenin alanını anlamak açısından oldukça faydalıdır. Bu formül, eşkenar üçgenin yükseklik formülü ile desteklenmektedir.
Eşkenar Üçgenin Alanı
Milda, eşkenar üçgenin alanını hesaplamak için yükseklik kullanmanın gerçekten etkili bir yöntem olduğunu belirttiniz. Yüksekliği bularak A = (1/2) a h formülünü uygulamak, üçgenin alanını anlamak açısından önemli bir adım.
Yükseklik Hesabı
Eşkenar üçgende yükseklik, kenar uzunluğu ile doğrudan ilişkilidir. Kenar uzunluğunu a olarak alırsak, yükseklik h = (√3/2) a formülü ile hesaplanabilir. Bu yükseklik, üçgenin tabanına dik bir şekilde inerek alan hesaplamasına katkıda bulunur.
Sonuç
Sonuç olarak, bu yöntem sadece alan hesaplamakla kalmaz, aynı zamanda üçgenin geometrik özelliklerini de anlamamıza yardımcı olur. Eşkenar üçgenin simetrik yapısı, yükseklik hesaplaması ile birlikte alanın daha iyi kavranmasına olanak tanır. Yorumlarınız için teşekkür ederim!
Dikdörtgen alan hesaplama konusunda zorlandığınızda, eğer kenar uzunlukları belli ise basit bir formül kullanarak sonuç bulabilirsiniz. Alan A = uzunluk x genişlik formülü ile kolayca hesaplama yapabilirsiniz. Geometri derslerinde bu tür sorular sıkça çıkıyor, pratik yapmak önemli.
Değerli Atasagun,
Dikdörtgen alan hesaplama konusunda yaşadığınız zorlukları anlıyorum. Geometri, özellikle alan hesaplamaları, başlangıçta karmaşık görünebilir. Ancak belirttiğiniz gibi, kenar uzunlukları bilindiğinde A = uzunluk x genişlik formülü ile işlemi oldukça basit hale getiriyoruz. Pratik yapmak, bu tür soruların üstesinden gelmenin en etkili yoludur.
Daha fazla pratik yaparak, farklı dikdörtgenlerin alanlarını hesaplayarak bu konudaki yetkinliğinizi artırabilirsiniz. Ayrıca, geometri derslerinde öğretmeniniz veya arkadaşlarınızla bu konuyu tartışmak size yardımcı olabilir. Herkese açık kaynaklardan faydalanarak çeşitli problemler çözmek, konuyu daha iyi anlamanızı sağlayacaktır. Başarılar dilerim!
Eşkenar üçgenin alanını bulmak için en yaygın yöntemlerden biri, üçgende benzerlik alan formülü kullanmaktır. Kenar uzunluğuna dayanan A = (√3 / 4) a² formülü, eşkenar üçgenin alanını hesaplamak için oldukça etkilidir. Bu formülü öğrenmek, geometri derslerinde büyük avantaj sağlar.
Pekdemir, yorumunuz için teşekkür ederim. Eşkenar üçgenin alanını bulmak için verdiğiniz formül gerçekten de oldukça kullanışlı ve yaygın olarak kullanılan bir yöntemdir. Geometri derslerinde bu tür formülleri öğrenmek, hem pratik hem de teorik anlamda önemli bir avantaj sağlar. Özellikle benzerlik prensiplerini anlamak, üçgenler gibi temel geometrik şekillerin özelliklerini daha iyi kavramamıza yardımcı olur. Alan hesaplamalarıyla ilgili daha fazla bilgi paylaşmak isterseniz, tartışmaya devam edebiliriz.
Eşkenar üçgenin alanını hesaplama yöntemleri hakkında bilgi verirken, en boy yükseklik hesaplama konusunu da göz önünde bulundurmak önemli. Yükseklik hesaplanarak alanın bulunması, üçgenin geometrik özelliklerini anlamak açısından faydalı. Bu şekilde, matematiksel uygulamaların günlük hayatta nasıl karşımıza çıktığını daha iyi kavrayabiliriz.
Alan Hesaplama Yöntemleri
Eşkenar üçgenin alanını hesaplamak için birkaç yöntem bulunmaktadır. En yaygın kullanılan yöntemlerden biri, bir kenarın uzunluğunu bilerek alanı hesaplamaktır. Eşkenar üçgenin alanı, kenar uzunluğu 'a' ise şu formülle hesaplanır:
\[ \text{Alan} = \frac{\sqrt{3}}{4} \times a^2 \]
Bu formül, üçgenin tüm kenarlarının eşit olması nedeniyle oldukça pratiktir.
Yükseklik Hesaplama
Eşkenar üçgenin yüksekliğini hesaplamak da alan hesaplamasında önemli bir adımdır. Yükseklik, üçgenin tabanına dik bir şekilde inen doğru parçasıdır. Yükseklik hesaplamak için yine kenar uzunluğundan faydalanabiliriz. Yükseklik 'h' şu şekilde hesaplanır:
\[ h = \frac{\sqrt{3}}{2} \times a \]
Bu yükseklik, alan hesaplamasında kullanılarak, alanın bir diğer formülü olan:
\[ \text{Alan} = \frac{1}{2} \times \text{Taban} \times \text{Yükseklik} \]
şeklinde ifade edilebilir.
Günlük Hayatta Uygulama
Eşkenar üçgenin alan ve yükseklik hesaplamaları, günlük hayatımızda birçok alanda karşımıza çıkmaktadır. Örneğin, mimari tasarımlar, bahçe düzenlemeleri veya sanatsal çalışmalar gibi pek çok alanda bu bilgileri kullanarak daha etkili ve estetik yapılar oluşturabiliriz. Matematiksel uygulamaların pratikteki yeri, bu tür hesaplamalarla daha iyi anlaşılmaktadır. Rüvide, bu konudaki düşüncelerinizi paylaştığınız için teşekkür ederim.
Dik üçgen alan hesaplama konusunda yaşadığım deneyimler oldukça öğreticiydi. Dik kenar uzunluklarının çarpımını yarıya bölerek alanı bulmak, pratikte çok işe yarıyor. Matematiksel formüller ile bu tür hesaplamalar yaparken, sürecin basitliği beni her zaman etkiliyor.
Koçer,
Dik Üçgen Alan Hesaplamanın Önemi
Dik üçgenlerin alanını hesaplamak, geometrik ve pratik uygulamalarda oldukça önemlidir. Dik kenar uzunluklarının çarpımını yarıya bölerek alanı bulma yöntemi, hem basit hem de etkili bir yöntemdir. Bu formül sayesinde, karmaşık hesaplamalar yapmadan hızlı bir şekilde sonuç alabiliyoruz.
Matematiğin Basitliği
Matematiksel formüllerin sağladığı bu basitlik, öğrenme sürecini daha keyifli hale getiriyor. Özellikle temeldeki bu tür pratik bilgilerin, daha karmaşık matematiksel kavramları anlamamızda nasıl bir köprü görevi gördüğünü görmek oldukça öğretici.
Pratik Uygulamalar
Dik üçgen alan hesaplama, mimarlık, mühendislik ve günlük hayatta birçok alanda karşımıza çıkıyor. Dolayısıyla, bu tür temel matematik bilgilerini iyi bilmek, hem akademik hem de pratik yaşamda büyük avantaj sağlıyor.
Deneyimlerinizi paylaştığınız için teşekkürler!
İkizkenar üçgenin iç açıları toplamı hakkında bir soru sormak istiyorum. İkizkenar üçgenin taban açıları eşit olduğu için bu açıların toplamı ve tepe açısını bulmak, üçgenin özelliklerini anlamak için çok önemli. Bu konuda daha fazla bilgi almak isterim.
İkizkenar Üçgenin İç Açıları Toplamı
İkizkenar üçgenin iç açıları toplamı, her üçgenin iç açıları toplamı gibi 180 derecedir. İkizkenar üçgende, taban açıları eşit olduğundan, bu açıların her birine 'x' diyelim. Tepe açısını ise 'y' ile gösterelim. Bu durumda, aşağıdaki denklemi kurabiliriz:
x + x + y = 180
2x + y = 180
Taban Açıları ve Tepe Açısı
Buradan tepe açısını bulmak için, 2x ifadesini 180'den çıkarabiliriz:
y = 180 - 2x
Bu formül sayesinde, taban açılarını bildiğinizde tepe açısını hesaplayabilirsiniz. Örneğin, taban açıları 50 derece ise:
y = 180 - 2(50) = 80 derece olur.
Örnek Üzerinden Açıklama
Eğer bir ikizkenar üçgenin taban açıları 60 derece ise:
y = 180 - 2(60) = 60 derece.
Bu durumda, ikizkenar üçgeniniz aynı zamanda eşkenar üçgendir.
Bu bilgiler, ikizkenar üçgenin özelliklerini anlamanız açısından oldukça faydalı olacaktır. Başka bir sorunuz varsa memnuniyetle yanıtlarım.
Üçgende yükseklik bulma konusu oldukça önemli. Bir üçgenin alanını hesaplarken yükseklik ve taban uzunluğu birbirleriyle doğrudan ilişkilidir. Özellikle dik üçgenlerde yükseklik hesaplamak, alan bulmak için kritik bir adımdır. Bu konuyu anlamak, geometri bilgimizi derinleştiriyor.
Merhaba Rauf,
Üçgende yükseklik bulma konusu gerçekten de geometri açısından çok önemli bir konu. Yükseklik, bir üçgenin alanını hesaplamada en temel unsurlardan biri ve özellikle dik üçgenlerde bu hesaplamayı yapmak oldukça kolaylaşıyor.
Alan Hesabı için yükseklik ve taban uzunluğunun birlikte kullanılması gerektiğini belirttiğin gibi, bu ilişkiyi anlamak da üçgenlerin özelliklerini daha iyi kavramamızı sağlıyor. Geometri derslerinde bu tür temel kavramları öğrenmek, ileride daha karmaşık şekiller hakkında bilgi sahibi olmanın temelini oluşturuyor.
Eğer yükseklik hesaplamada veya üçgenlerin özelliklerinde daha fazla soru veya örnek varsa, bunları birlikte incelemek faydalı olabilir. Geometriyle ilgili bu tür konulara ilgi duyman harika!
Sevgiler.
Dik üçgende a kenarı 2a olan bir üçgen düşünün. Bu durumda, dik kenarların uzunluklarını kullanarak alan hesaplamak oldukça kolay. Alan formülü ile 2a uzunluğundaki kenarları çarptığımızda, sonuç mükemmel bir biçimde ortaya çıkıyor. Bu durum gerçekten heyecan verici!
Değerli Ülkü,
Dik üçgenin alanını hesaplamanın keyifli ve basit bir yolunu keşfetmişsiniz. 2a uzunluğundaki kenarların kullanılması, alan formülünün uygulanmasını gerçekten kolaylaştırıyor. Bu tür geometrik ilişkileri anlamak, matematiğin güzelliklerini daha da ortaya çıkarıyor. Ayrıca, üçgenin alanını bulmak için kullanılan formüllerin pratikteki yansımalarını görmek, matematiğe olan ilgiyi artırıyor. Böyle heyecan verici keşifler yapmak, öğrenme sürecini daha eğlenceli hale getiriyor. Bu konudaki düşüncelerinizi paylaşmanız, matematik tutkunuzun ne kadar büyük olduğunu gösteriyor. Daha fazla keşif yapmanızı dilerim!
Ãçgenin alanını hesaplamak için taban uzunluğu ve yüksekliği ölçtüm ama neden sadece bu iki değerin çarpımının yarısı bize alanı verir? Diğer kenar uzunluklarını hesaba katmıyor muyuz?
Alan Hesabı ve Üçgenin Özellikleri
İzem, üçgenin alanını hesaplamak için taban uzunluğu ve yüksekliğin çarpımını yarıya bölmemiz, üçgenin geometrik yapısından kaynaklanmaktadır. Üçgen, bir taban ve o tabana dik bir yükseklik ile tanımlanan bir şekildir. Taban uzunluğu, üçgenin alt kenarını temsil ederken, yükseklik ise bu tabana dik olan en kısa mesafedir.
Üçgenin Özellikleri
Üçgenin diğer kenar uzunlukları, alan hesaplamasında doğrudan etkili değildir çünkü alan, yalnızca taban ve yükseklik ile tanımlanır. Üçgenin alanı, bir dikdörtgenin alanına benzer şekilde hesaplanır. Dikdörtgenin alanı, uzunluk ve genişliğin çarpımı ile bulunurken, üçgenin alanı bu dikdörtgenin yarısıdır. Yani, üçgenin tabanı ile yüksekliği çarptığınızda, aslında o üçgenin oluşturduğu dikdörtgenin alanını bulmuş olursunuz, bu nedenle sonucu ikiye bölerek gerçek üçgen alanını elde ederiz.
Sonuç
Bu nedenle, üçgenin alanını hesaplarken sadece taban ve yükseklik yeterli olur. Diğer kenar uzunlukları, üçgenin şekli hakkında bilgi verse de, alan hesaplamasında bu iki değer belirleyicidir.
- 23 Eylül 2024 Pazartesi
Eşkenar Üçgenin Alanı Nasıl Hesaplanır?- 19 Eylül 2024 Perşembe
75 15 90 Üçgeni Açılarına Göre Özel Dik Üçgenler- 30 Eylül 2024 Pazartesi
Üçgenin Yardımcı Elemanları Nelerdir?- 22 Eylül 2024 Pazar
Eşkenar Üçgenin Özellikleri- 23 Eylül 2024 Pazartesi
Dik Üçgen Özellikleri Nelerdir?