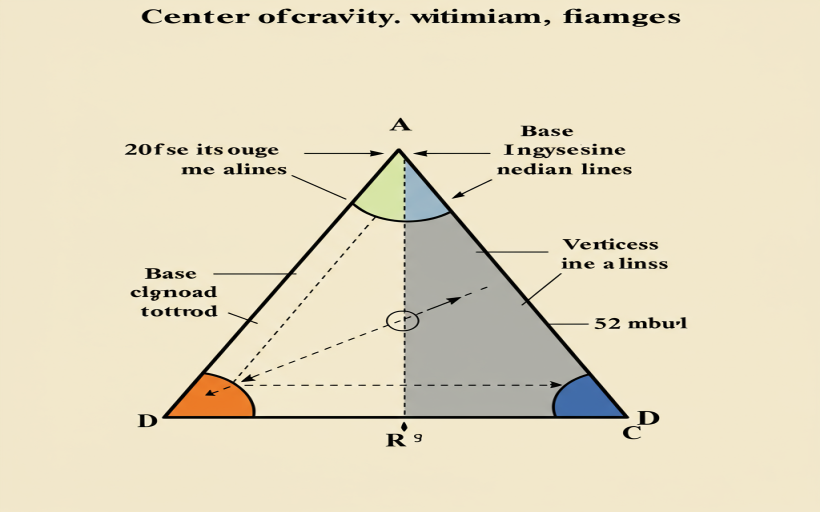
Ağırlık merkezi üçgen nasıl hesaplanır?

Ağırlık merkezi, bir nesnenin veya sistemin kütle veya hacim dağılımına göre denge noktasıdır. Üçgenler için ağırlık merkezi, üçgenin köşelerinin belirli bir oranına göre hesaplanır ve geometri ile fizik arasında önemli bir köprü görevi görür. Bu makalede, bir üçgenin ağırlık merkezinin nasıl hesaplandığına dair detaylı bir inceleme sunulacaktır.

Ağırlık merkezi, bir nesnenin tüm kütlesinin veya hacminin dengede olduğu noktadır. Üçgenler için ağırlık merkezi, üçgenin köşe noktalarının kesişiminden elde edilir ve genellikle "G" harfi ile gösterilir. Üçgenin ağırlık merkezi, üçgenin kenar orta noktalarının kesişim noktasında bulunur ve bu nokta, üçgenin her bir köşesinin eşit uzaklıkta bulunduğu bir noktadır.

Bir üçgenin ağırlık merkezini hesaplamak için aşağıdaki adımlar izlenebilir:

• Üçgenin köşe noktalarını belirleyin: A(x1, y1), B(x2, y2), C(x3, y3).
• Ağırlık merkezinin x ve y koordinatlarını hesaplayın
• xG = (x1 + x2 + x3) / 3
• yG = (y1 + y2 + y3) / 3

Bu formüller, üçgenin köşe noktalarının x ve y koordinatlarının ortalamasını alarak ağırlık merkezinin konumunu belirler.

Bir örnek üzerinden açıklamak gerekirse, A(2, 3), B(6, 5) ve C(4, 1) üçgenine bakalım.

• Öncelikle köşe noktalarını belirleyelim: x1 = 2, y1 = 3; x2 = 6, y2 = 5; x3 = 4, y3 = 1.
• Ağırlık merkezinin x koordinatını hesaplayalım

xG = (2 + 6 + 4) / 3 = 12 / 3 = 4

• Ağırlık merkezinin y koordinatını hesaplayalım

yG = (3 + 5 + 1) / 3 = 9 / 3 = 3Bu durumda, Ağırlık Merkezi G(4, 3) noktasıdır.

Ağırlık merkezi ile ilgili bazı önemli özellikler şunlardır:

• Ağırlık merkezi, üçgenin kenar orta noktalarını birleştiren üç çizginin kesişim noktasında bulunur.
• Ağırlık merkezi, üçgenin her bir köşesinden kenarlara olan uzaklıkların toplamının eşit olduğu bir noktadır.
• Ağırlık merkezi, üçgenin simetri eksenleri boyunca daima iç kısımda yer alır.

Ağırlık merkezi hesaplamaları, mühendislik, mimarlık ve fizik gibi birçok alanda önemli bir yere sahiptir. Özellikle yapıların stabilitesinin sağlanması, nesnelerin dengelenmesi ve mühendislik tasarımlarının optimize edilmesi açısından kritik bir öneme sahiptir. Ayrıca, ağırlık merkezi hesaplamaları, bilgisayar grafiklerinde ve oyun tasarımında da yaygın olarak kullanılmaktadır.

Ağırlık merkezi, üçgenlerin geometrik özelliklerini anlamak için temel bir kavramdır. Üçgenin köşelerini kullanarak yapılan hesaplamalar, hem teorik hem de pratik uygulamalarda önemli bir rol oynamaktadır. Ağırlık merkezinin doğru bir şekilde tespit edilmesi, birçok mühendislik ve fiziksel probleme çözüm bulmak için gereklidir. Bu nedenle, ağırlık merkezi hesaplamaları, matematiksel geometri ve mühendislik alanında önemli bir yer tutmaktadır.